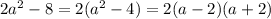
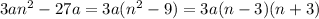
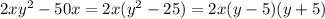
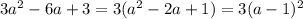
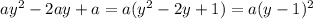
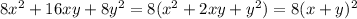
При каких значениях параметра a уравнение
(5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0 имеет единственное решение
Решение : (5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0
Квадратное уравнение относительно 5ˣ > 0 || t = 5ˣ ||
D = (8a+5)² - 4(16a² +20a -14 )=64a² +80a +25 -64a² -80a+56 =81 =9² >0
т.е. это уравнение всегда имеет 2 решения
1. Если свободный член 16a² +20a - 14 будет отрицательный , то корни будут разных знаков и исходное уравнение будет иметь одно решение .
16a² +20a - 14 = 16(a +7/4)(a - 1/2) < 0 ⇒ a ∈ ( -7/4 ; 1/2 )
- - - - - - -
2. Второй случай свободный член 16a² +20a - 14 = 0
a = -7/4 или a = 1/2
уравнение принимает вид 5ˣ (5ˣ - 8a - 5) = 0, которое будет иметь
очевидно 5ˣ ≠ 0 , остается 5ˣ = 8a + 5 которое имеет решение если 8a + 5 > 0 ⇔ a > - 5 / 8 || a = 1/2 удовлетворяет ||
* * * -7/4 < -5/8 или 8*(-7/4 ) +5 = -14+5 = -9 < 0 * * *
Окончательно ответ: a ∈ ( -7/4 ; 1/2 ]
номер 2
Вводим переменную х и обозначаем так количество проданных помидоров во второй день. Запишем, сколько продано в первый и в третий день:
х * 80% = 0,8х (кг) – первый день;
х * 5/6 = 5х/6 (кг) – третий день.
Количество, проданное за три дня известно по условию. Составляем уравнение:
0,8х + х + 5х/6 = 158
4,8х + 6х + 5х = 948
15,8х = 948
х = 60 (кг) – второй день;
60 * 0,8 = 48 (кг) – первый день;
60 * 5/6 = 50 (кг) – третий день.
ответ: в каждый из трёх было продано 48 кг, 60 кг, 50 кг соответственно.
2) 2(a^2-4)=2(a-2)(a+2)
3) 3a(n^2-9)=3a(n-3)(n+3)
4) 2x(y^2-25)=2x(y-5)(y+5)
3(a^2-2a+1)=3(a-1)^2
a(y^2-2y+1)=a(y-1)^2.