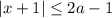
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если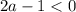 
, то есть 
.
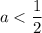Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если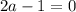 
, то есть 
.
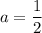Получаем неравенство:
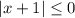
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
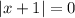
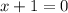
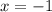
3. Если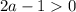 
, то есть 
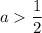, то получаем неравенство с положительной правой частью:
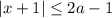
Заменим его следующим двойным неравенством:
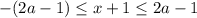
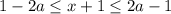
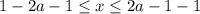
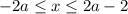
Таким образом получаем ответ:
при 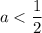: решений нет
при :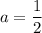
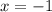
при 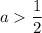: ![x\in[-2a;\ 2a-2]](/tpl/images/2004/6663/9d563.png)
делаете таблицу:
при х=1 у=-2
при х=3 у=0
2). у=1-3х
делаете таблицу:
при х=1 у=-2
при х=2 у=-5
Далее отмечаете эти точки на графике,
у вас получаются две прямые, точка пересечения
которых и будет ответом.