№1 (а)
ответ: -\frac{4}{3}" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=x%20%3E%20-%5Cfrac%7B4%7D%7B3%7D" title="x > -\frac{4}{3}">
№1 (б)
№2 (а)
-4} \atop {x\leq -2.5}} \right." class="latex-formula" id="TexFormula6" src="https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7Bx%3E-4%7D%20%5Catop%20%7Bx%5Cleq%20-2.5%7D%7D%20%5Cright." title="\left \{ {{x>-4} \atop {x\leq -2.5}} \right.">
№2(б)
\frac{36}{5}" class="latex-formula" id="TexFormula10" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
ответ: \frac{36}{5}" class="latex-formula" id="TexFormula12" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
Задание 1.
Треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны.
Иначе, для сторон a; b; c должны выполняться следующие три неравенства:
a+b>c; a+c>b; b+c>a
а) стороны равны a=10 см; b=15 см; c=25 см;
10+15=25
10+25>15
15+25>25
Три неравенства не выполняются, значит, треугольник не существует.
б) стороны относятся как 3:5:10;
a=3x; b=5x; c=10x;
3x+5x<10x;
3x+10x>5x
5x+10x>3x
Три неравенства не выполняются, значит, треугольник не существует.
Если сумма углов треугольника не равна 180 градусам, то треугольник не существует.
в) углы равны 46°, 64° и 80°;
46°+64°+80° = 190°
190°≠ 180° треугольник не существует.
г) углы относятся как 3:5:10.
3х+5х+10х=180°
18х = 180°
х = 180° : 18
х = 10°
3·10°=30°
5·10°=50°
10·10°=100°
30°+50°+100°=180°
Треугольник с углами 30°; 50°; 100° треугольник существует.
Задание 2.
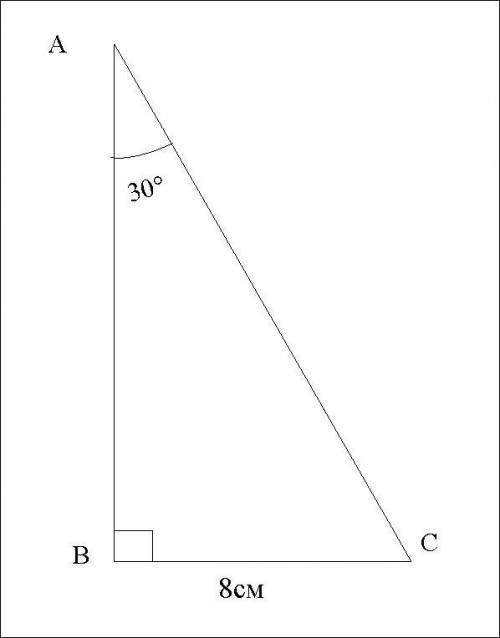
Перпендикуляр AB, наклонная AC и прямая ВС образовали прямоугольный ΔАВС.
∠А=30°;
ВС=8см.
Найти АС.
Решение
В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы.
У нас катет ВС лежит против угла величиной 30°, значит,
ВС = 1/2 АС.
А гипотенуза АС будет в 2 раза больше катета ВС.
АС = 2ВС
АС=2·8см
АС=16см
20/45=16/х
х=36
ответ:36кг