Функция у = х² + 4х - 12
График функции - квадратная парабола веточками вверх
Найдём характерные точки этой параболы.
1) Точка пересечения с осью Оу: х = 0; у = -12;
2) точки пересечения с осью Ох: у = 0
х² + 4х - 12 = 0
D = 4² - 4 · (-12) = 64
√D = 8
x₁ = (-4 - 8)/2 = -6
x₂ = (-4 + 8) = 2
Получили две точки (-6; 0) и (2; 0)
3) найдём координаты вершины С параболы С(m; n)
m = - b/2a = -4/2 = -2
n = y(-2) = (-2)² + 4 · (-2) - 12 = -16
C(-2; -16)
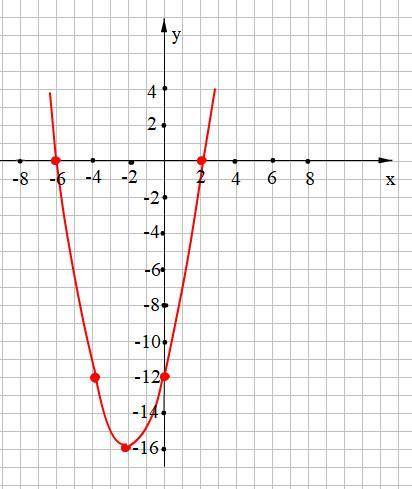
По найденным точкам строим параболу (смотри прикреплённый рисунок).
По графику находим
а) у > 0 при х ∈ (-∞; -6)∪(2; +∞); y < 0 при х ∈ (-6; 2)
б) у↑ при х ∈ (-2; +∞); у↓ при х ∈ (-∞; -2)
в) у наим = у(-2) = -16; наибольшего значения не существует.
x длина бокового ребра призмы(высота ) .
a² +x² = d² ⇒ a² = d² - x² ;
V(x) = (d² - x² ) x = d²x - x³ ;
V '(x) = d² - 3x² = -3( x +d/√3)(x -d/√3) ;
V '(x) - + -
( -d/√3 ) (d/√3 )
V(x) ↓ ↑ max ↓
V ' (x) =0 ⇒ x² =d²/3 ; x = d/√3 ; a² = d² - x² = d² - d²/3 = 2d²/3 ; a =√2d/√3 ; [x =a/√2 ].
ответ : d/√3 .
(ср ариф сред геом )