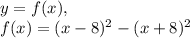
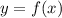— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 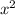(не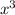 
, не 
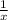, не 
и не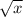 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид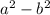 
, где 
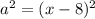, и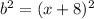 
. Формула «разность квадратов» раскрывается так: 
.
.
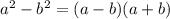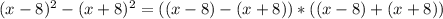
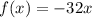, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
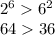
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
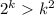
3) Тогда при n=k+1 должно выполняться неравенство:
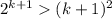
Вернемся к неравенству из второго пункта и домножим его на 2:
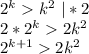
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
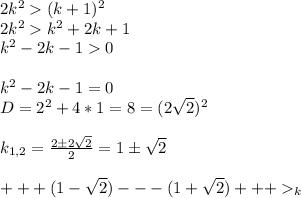
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если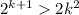 
, а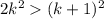 
, при k>5
То есть,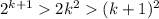 
, при k>5, то по закону транзитивности:
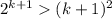, при k>5 - ч.т.д
