1) х² - 8х + 15 ≥ 0
Решаем уравнение
х² - 8х + 15 = 0
D = 8² - 4 · 15 = 4 = 2²
x₁ = 0.5(8 - 2) = 3
x₂ = 0.5( 8 + 2) = 5
Значения функции у = х² - 8х + 15 не отрицательны при х≤ х₁ и х≥ х₂
Неравенство имеет решение при х ∈ (-∞; 3] ∪ [5; +∞)
2) х² - 6х + 9 < 0
Преобразуем левую часть неравенства
(х - 3)² < 0
Квадрат любого числа неотрицателен, поэтому неравенство не имеет решений.
3) х² - 4х + 20 ≤ 0
Решаем уравнение
х² - 4х + 20 = 0
D = 4² - 4 · 20 = -64
Уравнение решений не имеет. Поэтому все значения функции у = х² - 4х + 20 положительны, и неравенство не имеет решений.
4) -х² + 7х - 12 < 0
Решаем уравнение
-х² + 7х - 12 = 0
D = 7² - 4 · 12 = 1
x₁ = -0.5(-7 + 1) = 3
x₂ = -0.5(-7 - 1) = 4
Значения функции у = -х² + 7х - 12 отрицательны при х > х₁ и х < х₂
Неравенство имеет решение при х ∈ (3; 4)
Объяснение:
Посчитаем:
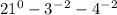
Тут выражение, равное разности степеней чисел 21 , 3 и 4
Свойство степени числа такое:
1. если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень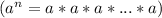 
.
2. если показатель равен нулю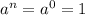 
3. если показатель меньше нуля, то пишем так: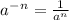 
Рассмотрим на нашем примере и посчитаем:
1) 21 в 0 степени - 1 по второму свойству.
2) 3 в степени -2 равно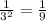 
по 3 свойству.
3) 4 в степени -2 равно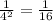 
по 3 свойству.
А затем выполним над ними операции, приведя к общему знаменателю:
144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.
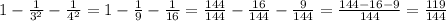
- положительное число, то есть число. которое больше 0. Что и требовалось доказать.
на втором и третьем месте -- любое из пяти цифр 0,1,...,4
значит всего чисел 4*5*5=100