Разложим знаменатель на множители:
Сумма коэффициентов равна нулю, значит корни уравнения 1 и -1/3.
Интеграл примет вид:
Разложим дробь, стоящую под знаком интеграла, на составляющие:
Дроби равны, знаменатели равны, значит равны и числители:
Многочлены равны, когда равны коэффициенты при соответствующих степенях. Составим систему:
Выразим из второго уравнения А:
Подставляем в первое и находим В:
Находим А:
Сумма принимает вид:
Значит, интеграл примет вид:
Для второго слагаемого выполним приведение под знак дифференциала:
Интегрируем:
Упрощаем:
Применим свойство логарифмов:
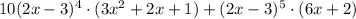
Объяснение:
Для начала необходимо понять, что данное выражение представляет собой произведение двух функций, а для производной от произведения функций существует правило:
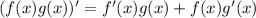
В данном случае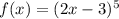 
, а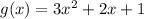 
Итак, нам потребуется производная от функции 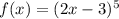, которая является сложной функцией, производная от которой берется по следующему правилу:
Здесь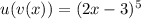 
, 
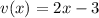
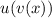- степенная функция, для нее правило такое:
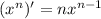
Вычисляем:
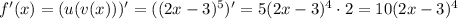
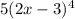мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от 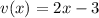. Т.е.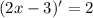 
---
Теперь возьмем производную от второго сомножителя в исходном выражении:
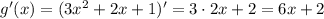
Подставляем все в формулу: ![\[(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]](/tpl/images/1008/0917/ca526.png)
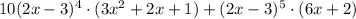
ответ: всего зо учеников