1) 8х + 1,3 = 34,9 - 8х 2) -4 = -2/8х
8х + 8х = 34,9 - 1,3 х = -4 : (-2/8)
16х = 33,6 х = 4 · 8/2
х = 33,6 : 16 х = 2 · 8
х = 2,1 х = 16
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3) 9х = 108 4) 6х - 8 = 6,4
х = 108 : 9 6х = 6,4 + 8
х = 12 6х = 14,4
х = 2,4
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
5) 4(х - 2) = -1 6) 40х = -32
4х - 8 = -1 х = -32 : 40
4х = 8 - 1 х = -0,8
4х = 7
х = 7/4
х = 1 целая 3/4 = 1,75 (в десятичных дробях)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
7) 4х - 2 = 22 8) 5х - 13 + 2(3 - х) = -х + 16
4х = 22 + 2 5х - 13 + 6 - 2х = -х + 16
4х = 24 5х - 2х + х = 16 - 6 + 13
х = 24 : 4 4х = 23
х = 6 х = 23/4 = 5 целых 3/4 = 5,75
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
9) 4(3х + 5) - 3(4х - 1) = 22х + 12
12х + 20 - 12х + 3 = 22х + 12
12х - 12х - 22х = 12 - 3 - 20
-22х = -11
х = -11 : (-22)
х = 1/2 = 0,5 (в десятичных дробях)
Номер 1
1) D(x) = R, кроме (-8) и 12
2) D(x) = R, кроме (-9) и 2
3) D(x) = R, кроме 2
Номер 2
1) 3,5
2) 0
3) 2,6
Номер 3
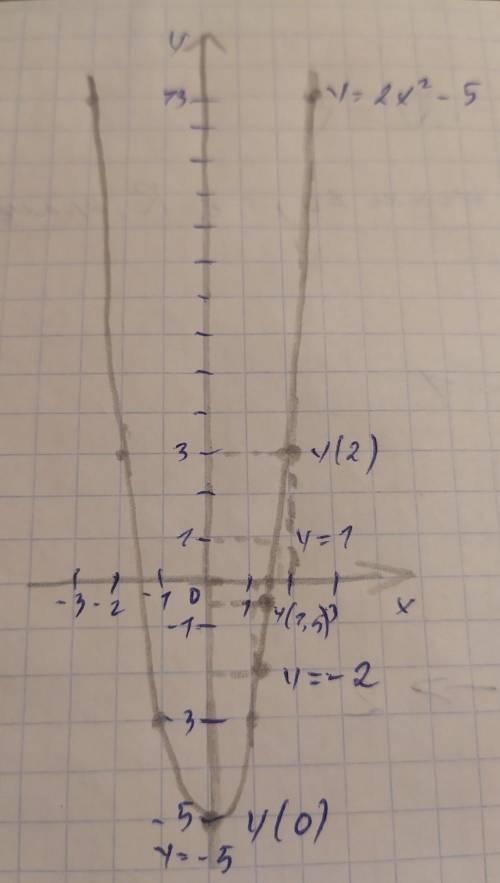
x: -3; -2; -1; 0; 1; 3.
y: 13; 3; -3; -5; -3; 13.
а) y(2) = 3; y(-1,5) = -0,5; y(0) = -5
б) при y = -5, x = 0; при y = -2, x ≈ 1,2; при y = 1, x ≈ 1,7
в) D(x) = R; E(y) = [-5;+∞)
г) при A(-20;795) x = -20 y = 795, проверим, подставив x в уравнение функции: y = 2*(-20)^2-5=795; 795=795, значит A принадлежит y=2x^2-5
при B(10;205) x=10, y=205, проверим: y=2*(10)^2-5=195; 195≠205, значит B не принадлежит y=2x^2-5
-2sinx *cos4x = 0 ;
[ sinx =0; cos4x =0. [ x =π*k ; 4x =π/2 +π*k , k∈Z. [ x =π*k ; x =π/8 +π/4*k , k∈Z.
ответ :: π*k ; π/8 +π/4*k , k∈Z .
2sin2x +5sinx =0;
2*2sinx*cosx +5sinx =0 ;
4sinx(cosx +5/4) = 0 ;
[sinx =0 ; cosx +5/4 =0 . [sinx =0 ; cosx = -5/4 < -1 (не имеет решения) .
sinx =0 ;
x =π*k ,k∈Z.
ответ : π*k ,k∈Z.
sin2x +cos²x =0;
2sinx*cosx +cos²x =0;
2cosx(sinx +1/2cos x) =0 ; * * * [ cosx =0 ;sinx +1/2cosx =0. * * *
a) cosx =0 ;
x =π/2 +π*k ; k∈Z.
b) sinx +1/2cos x =0;
sinx = -1/2cos x *** cosx ≠0 ***
tqx =-1/2 ;
x = -arctq(1/2) +π*k k∈Z .
ответ : arctq(1/2) +π*k , k∈Z .
8cos²x - 10sinx -11 = 0 ;
8(1 - sin²x) -10sinx -11 = 0 ;
8sin²x +10sinx +3 =0 ; замена : t=sinx.
8t² +10t +3 =0 ;
D/4 =5² -8*3 =1² .
t₁ = (- 5 -1)/8 = - 3/4 ;
t ₂= (- 5 +1)/8 =- -1/2.
sinx₁= -3/4;
x₁= (-1)^(n+1)arcsin(3/4) +π*k ,k∈Z ;
sinx₂= -1/2 ;
.x₂ = (-1)^π/6 +π*k ,k∈Z .
ответ : (-1)^(n+1)arcsin(3/4) +π*k , (-1)^(n+1)*π/6 +π*k , k∈ Z ;
жадная