Объяснение:
1а) x² + x - 20 ≠0
найдем x² + x - 20 = 0
D = 1+80 = 81
x ₁ ₂ = (-1 ±9) / 2
x₁ = -5
x₂ = 4
ОВФ (-∞; -5)∩ (-5;4)∩(4; +∞)
1б) получитсясистема:
{x+9 ≥0 {x≥-9
{4-x ≥0 {x ≤4
ОВФ [-9;4]
2a) f(-x) = -4x⁷ +2x³ = -f(x) нечетная
2б) f(-x) = (-x)² -3(-x)⁴= x² -3x⁴ = f(x) четная
2в) f(-x) = -x³ + (-x)⁶ = -x³ + x⁶ ≠ f(x) ≠ f(x) ни четная, ни нечетная
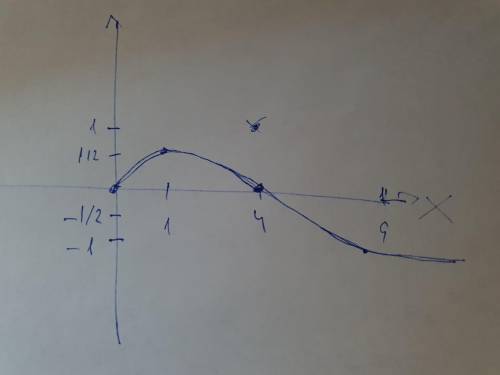
3) область определения X≥0
а) пересечение с x т. е. y =0 при х = 0 и x = 4 точки (0;0), (4;0)
б) возрастание [0;1]
убывание (1;+∞)
в) ОЗФ, [0.5; +∞)
Нехай батончик коштує х грн, а плитка шоколаду – у грн. Тоді сім батончиків коштують 7х грн, а дві плитки шоколаду – 2у грн. Оскільки ралом за таку кількість батончиків і плиток шоколаду заплатили 59 грн, маємо рівняння: 7х + 2у = 59.
Вартість трьох батончиків складає 3х грн, і вони дорожчі за плитку шоколада на 3 грн. Тому одержимо ще одне рівняння: 3х – у = 3.
Щоб відповісти на запитання задачі, ми маємо знайти такі значення х і у, які б задовольняли обидва рівняння, тобто задовольняли систему рівнянь:
Розвязування задач за до систем лінійних рівнянь
Розв’язавши цю систему, одержимо, що х = 5; у
= 12. Отже, вартість шоколадного батончика – 5 грн, а вартість плитки шоколаду – 12 грн.
В і д п о в і д ь: 5 грн; 12 грн.
Объяснение: так