ЗАДАЧА:
Расстояние от точки А до точки В= 62 км. На расстоянии 30 км от точки А находится точка С. Из точки А в точку С выехал велосипедист со скоростью 12км/ч, а через 30 минут из точки В в точку С выехал мотоциклист.
ВОПРОС 1: с какой скоростью должен ехать мотоциклист, чтобы встретиться с велосипедистом в точке С?
ВОПРОС 2:
С какой скоростью должен ехать мотоциклист, чтобы приехать в точку С раньше велосипедиста на 1 час 10 минут?
Объяснение:
если от точки А до точки С 30км, то от точки
С до В=62–30=32км. Поэтому велосипедисту до точки С нужно проехать 30км, а мотоциклисту из точки В до точки С - 32 км
Велосипедист со скоростью 12км/ч проедет расстояние 30км за: 30÷12=5/2=2,5 часа
1 ч 10 мин=1 целая 1/6часа или 7/6часа.
Чтобы мотоциклист доехал до точки С раньше велосипедиста на 7/6часа, тогда:
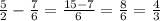
Итак: мотоциклисту нужно добраться до точки С за 4/3 часа. Для этого ему понадобится:
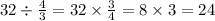
ОТВЕТ 2: мотоциклисту нужно ехать со скоростью 24км/ч, чтобы приехать раньше велосипедиста на 1 час 10 минут.
РЕШЕНИЕ Вопроса 1
30минут=1/2=0,5 часа
Так как мотоциклист выехал через 30 минут после
велосипедиста, то велосипедист за 30 минут проехал: 12÷2=6км и ему осталось проехать 30–6=24км и ему понадобится на это:
2,5 –0,5=2часа.
Соответственно мотоциклисту до встречи с велосипедистом в точке С понадобится также 2часа.
Мотоциклисту нужно за 2 часа проехать 32 км, поэтому ему нужно ехать со скоростью: 32÷2=16км/ч
ОТВЕТ 1: чтобы встретиться с велосипедистом в точке С мотоциклисту нужно ехать со скоростью 16км/ч
№4
найдем нули функции
0=х²-4х+3
D=(-4)²-4×3×1=4
x=(4±√4)÷2= 3 или 1
a=1>0⇒ ветви параболы вверх ⇒ y>0 x∈(-∞;1)∪(3;∞)
y<0 (1;3)
№6
я тебе график не построю но с аргументом
также находим нули функции
0=х²-4
0=(х-2)(х+2) ⇒х=±2
а=1>0 ⇒ ветви параболы вверх ⇒y>0 (-∞;-2)∪(2;∞)
№5
y=-x²+6x-5
найдем ось симметрии m=-b/2a=-6÷(2×(-1))=3
a=-1<0 ⇒ ветви вниз ⇒ функция возрастает (-∞;3)
функция убывает(3;∞)
№7
g(x)=-4x²+16x-3
a=-4<0 ⇒ ветви вниз ⇒ самое наибольшее значение y будет получаться при самом наименьшем значении х ⇒ряд по убыванию таков: f(2) , f(5) ,f(8.1) , f(11.8)
ответ: 20 км/ч.
Объяснение: Пусть х км/ч скорость мотоциклиста, тогда скорость велосипедиста х-10 км/ч. Время за которое мотоциклист затратил на весь путь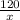
часов, а велосипедист 
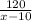часов. Разница во времени составила 6 часов. Составим уравнение:
х₁=(-10) (км/ч) не подходит, т.к. скорость не может быть отрицательной.
х₂=20 (км/ч) скорость мотоциклиста.