и 
. Чтобы найти для них общий знаменатель, нужно найти найменьшее общее число которое нацело делилось бы на знаменатель первого и второго дроба, в даном случае знаменатели это 25 и 4. Ну можно взять больший знаменатель умножить на 2 и проверить делится ли это число нацело на первый и другой знаменатель, если не делится ужножаеш на 3 и проверяеш, и так далее. Часто бывает, что один с знаменателей уже делится на себя и на второй знаменатель, тогда это и будет общий знаменатель. Потом оно само будет получаться, потому что будешь знать что на что делится.+ ;
;
= 
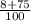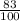, если можно сократить (то есть и числитель и множитель делится на одинаковое число), то сокращаем.
1)комиссия состоит из 3-х человек.
2) в комиссию может войти
а) один из 6-ти десятиклассников и 2 из 8-и одиннадцатиклассников
б) ни одного десятиклассника (т.к. понятие не более - это значит равно и меньше. Для людей - это 1 либо 0). Тогда в комиссии будут только 3 одиннадцатиклассника.
Решаем
а) 2 из 8 одиннадцатиклассников = 8!/(2!*(8-2)!) =28 но на каждого из 6 десятикл. приходится 28 комбинаций из 2-х одиннадцатикл. , соответственно комиссию можно составить
б) 3 из 8 одиннадцатикл. = 8!/(3!*(8-3)!)=56
т.е. всего возможных комбинаций при заданном условии задачи будет