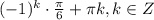
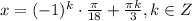
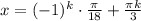
1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
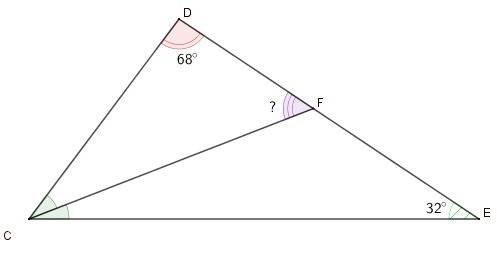
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°
1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°

cos a - cos b = -2sin ((a+b)/2)*sin ((a-b)/2)
В нашем случае
cos 2x - cos 8x = -2sin 5x*sin (-3x) = 2sin 5x*sin 3x
Получаем уравнение
2sin 5x*sin 3x = sin 5x
1) sin 5x = 0, 5x = pi*k, x = pi/5*k
На промежутке [0, pi] будут корни 0, pi/5, 2pi/5, 3pi/5, 4pi/5, pi - 5 корней
2) 2sin 3x = 1, sin 3x = 1/2,
3x = pi/6 + 2pi*n, x = pi/18 + 2pi/3*n = pi/18 + 12pi/18*n
На промежутке [0, pi] будут корни pi/18, 13pi/18 - 2 корня
3x = 5pi/6 + 2pi*m, x = 5pi/18 + 2pi/3*m = 5pi/18 + 12pi/18*m
На промежутке [0, pi] будут корни 5pi/18, 17pi/18 - 2 корня.
Всего 9 корней.