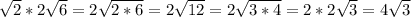
Объяснение:
1.
x - скорость катера, км/ч.
5/(x+3) +8/x=1
(5x+8(x+3))/(x(x+3))=1
5x+8x+24=x²+3x
x²+3x-13x-24=0
x²-10x-24=0; D=100+96=196
x₁=(10-14)/2=-4/2=-2 - ответ не подходит по смыслу.
x₂=(10+14)/2=23/2=12 км/ч - скорость катера.
2.
За единицу примем объём бассейна.
x - время заполнения бассейна 1-й трубой, ч.
1/x +1/(x+15)=1/10
(x+15+x)/(x(x+15))=1/10
10(2x+15)=x²+15x
x²+15x-20x-150=0
x²-5x-150=0; D=25+600=625
x₁=(5-25)/2=-20/2=-10 - ответ не подходит по смыслу.
x₂=(5+25)/2=30/2=15 ч - время заполнения бассейна 1-й трубой.
3.
a²+b²=c², где
a,b - катеты; с - гипотенуза.
(c-1)²+(c-8)²=c²
c²-2c+1+c²-16c+64=c²
2c²-18c+65-c²=0
c²-18c+65=0; D=324-260=64
c₁=(18-8)/2=10/2=5 - ответ не подходит, если 2-й катет меньше гипотенузы на 8, то он должен составлять: 5-8=-3, что не подходит по смыслу.
c₂=(18+8)/2=26/2=13
4.
a²+b²=c², где
a - длина; b - ширина; с - диагональ.
(b+3)²+b²=15²
b²+6b+9+b²-225=0
2b²+6b-216=0 |2
b²+3b-108=0; D=9+432=441
b₁=(-3-21)/2=-24/2=-12 - ответ не подходит по смыслу.
b₂=(-3+21)/2=18/2=9 - ширина.
9+3=12 - длина (большая сторона).
![\[\left\{\begin{aligned}&(a-1) x^2 - 2x - a 0, \\[1ex] &x 3.\end{aligned}\right.\]](/tpl/images/4978/1345/169ad.png)
Рассмотрим сначала особую точку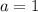 
--- там парабола вырождается в прямую. Тогда
![\[\left\{\begin{aligned}&{-2x}-1 0, \\ &x 3\end{gathered}\right.\implies x\in\varnothing.\]](/tpl/images/4978/1345/2d85f.png)
Значит, все дальнейшие рассуждения проводим при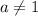 
.
Найдём корни функции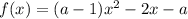 
:
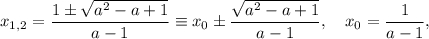
где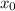 
--- вершина параболы и по совместительству точка экстремума функции 
.
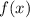Значение функции в этой точке равно
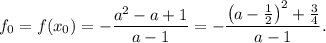
Из исследования знаков производной/функции легко установить, что при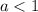 
величина 
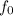--- максимум (это, впрочем, понятно и из вида функции 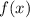), больший нуля. Причём в этом случае 
, т.е. понятно, что в области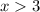 
функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения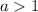 
.
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим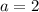 
.
Корни и точка экстремума:
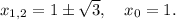
Теперь уже 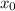- минимум функции, а (после аналогичного анализа) 
.
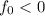Если нам повезёт, то правый (который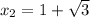 
) корень будет лежать левее точки 
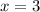, а это будет означать, что к тому времени как функция подойдёт к 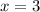, она уже будет положительна (ведь правее экстремума 
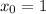парабола рогами вверх будет идти только вверх). Исследуем:
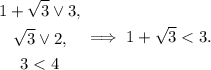
Победа.
ответ. .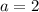
