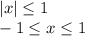
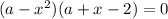
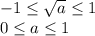
![a \in [0;1]](/tpl/images/0775/0492/4bfc3.png)
- неравенства будут иметь общее решение, значит при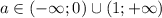 
неравенства общих решений не будет иметь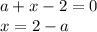
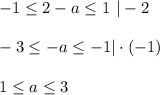
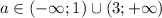неравенства общих решений не имеют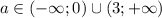
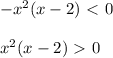
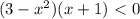
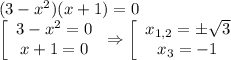
![a \in (-\infty;0]\cup[3;+\infty)](/tpl/images/0775/0492/a3d1e.png)
19320
Объяснение:
Обозначим сумму
S=40+41+42+...+198+199+200.
Вычислим сумму двумя Отметим, что в сумме количество слагаемых равен (200-40)+1=161.
Выражения для суммы напишем двумя и суммируем почленно:
S= 40 + 41 + 42 +...+198+199+200
S=200+199+198+...+ 42 + 41 + 40
Тогда:
2·S=(40+200)+(41+199)+(42+198)+...+(198+42)+(199+41)+(200+40)=
=240+240+240+...+240+240+240=161·240=38640.
Отсюда
S=38640:2=19320.
Можем рассмотреть сумму как сумма членов арифметической прогрессии с первым членом a₁=40 и d=1. Применим формулу для суммы первых n-членов арифметической прогрессии:
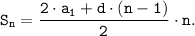
Так как n=161, то
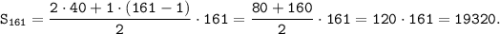
=e^(x-11)*(5x²-25x+20)=0
5(x²-5x+4)=0
x1+x2=5 U x1*x2=4
x1=1 U x2=4
+ _ +
1 4
max min
y(1)=(5-35+55)e^(-10)=25/e^10 наиб
y(4)=(80-140+55)e^(-7)=-5/e^7 наим