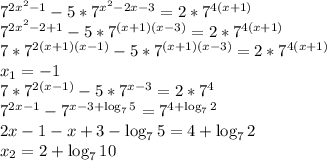
Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
Номер 1
1) D(x) = R, кроме (-8) и 12
2) D(x) = R, кроме (-9) и 2
3) D(x) = R, кроме 2
Номер 2
1) 3,5
2) 0
3) 2,6
Номер 3
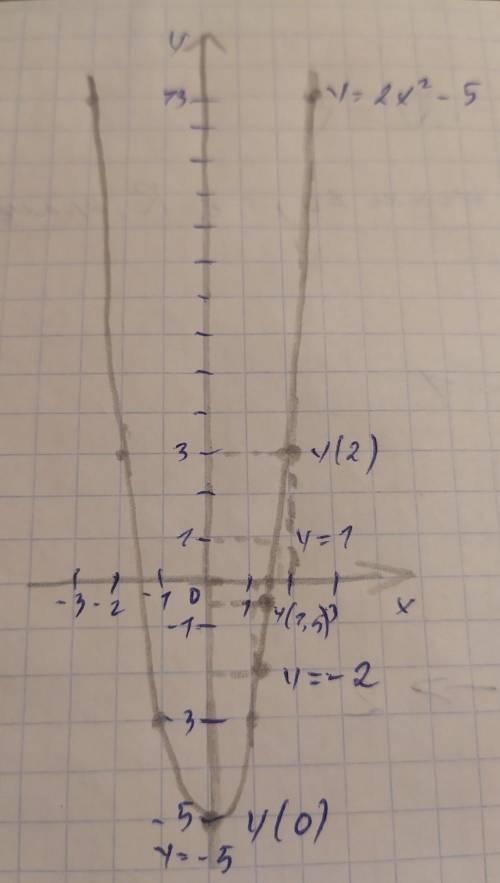
x: -3; -2; -1; 0; 1; 3.
y: 13; 3; -3; -5; -3; 13.
а) y(2) = 3; y(-1,5) = -0,5; y(0) = -5
б) при y = -5, x = 0; при y = -2, x ≈ 1,2; при y = 1, x ≈ 1,7
в) D(x) = R; E(y) = [-5;+∞)
г) при A(-20;795) x = -20 y = 795, проверим, подставив x в уравнение функции: y = 2*(-20)^2-5=795; 795=795, значит A принадлежит y=2x^2-5
при B(10;205) x=10, y=205, проверим: y=2*(10)^2-5=195; 195≠205, значит B не принадлежит y=2x^2-5