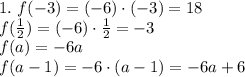
![y=f(x) = \left\{\!\begin{aligned} & 1, \ \ x\ \textless \ -1 \\ & x^2, \ \ -1 \leq x \leq 3 \\ \end{aligned}\right. \\ \\ \\ \\ -3 \in (-\infty;-1): \ \ f(-3)=1 \\ \\ -1 \in [-1;3]: \ \ \ f(-1)=(-1)^2=1 \\ \\ 3 \in [-1;3]: \ \ \ \ f(3)=3^2 =9](/tpl/images/0409/4054/4941b.png)
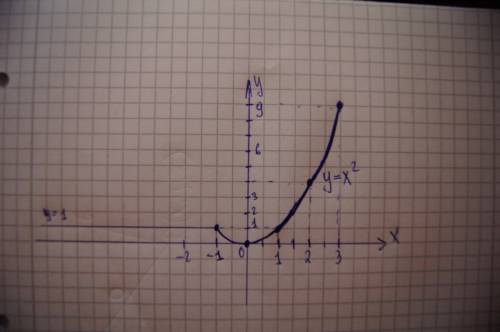
1) x∈(1;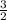 
)
2) x∈(-∞; -3)∪(1; +∞)
Объяснение первого неравенства:
Чтобы произведение было меньше нуля, множители должны иметь разные знаки. Тогда получаем две системы (знака системы сайт не имеет, строчки должны быть объединены фигурной скобкой).
Первая:
x-1<0
2x-3>0
Вторая:
x-1>0
2x-3<0
Решение первой:
x-1<0
x<1;
2x-3>0
2x>3
x>;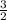
Поскольку мы решали систему, нужно найти пересечение решений. Здесь пересечение - пустое множество, потому что 3/2 больше 1.
Решение второй:
x-1>0
x>1;
2x-3<0
2x<3
x<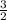
Пересечение решений - x∈(1; 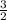) (скобки ставим круглые, потому что знак неравенства строгий)
Объяснение второго неравенства:
Чтобы произведение было больше нуля, множители должны иметь один знак. Тогда получаем две системы:
Первая:
x+3>0
x-1>0
Вторая:
x+3<0
x-1<0
Решение первой:
x+3>0
x>-3;
x-1>0
x>1;
Пересечение: x∈(1; +∞)
Решение второй:
x+3<0
x<-3;
x-1<0
x<1;
Пересечение: x∈(-∞; -3)
Пересекаем решения первой и второй систем и получаем: x∈(-∞; -3)∪(1; +∞)
1) х-3у =10 | 30+9у-2у=2
3х-2у=2 | 7у= -28
х= 10+3у | у= -4
3(10+3у)- 2у=2
у= -4
х= 10+3(-4)
у=-4
х=-2
2)х-3у=10 | 100+60у+9у^2-24у=100
х^2- 24у=100 | 9у^2+36у=0
х=10+3у | у(9у+36)=0
(10+3у)^2- 24у=100 | у=0 или 9у+36=0
у=4
если у=0, то х=10+3*0=10
если у=4, то х=10+3*4=22.
3)2х+3у=7 | 2х+9х-48=7
3х-у=16 | 11х=55
у=3х-16 | х=5
2х+3(3х-16)=7
х=5
у=3*5-16
х=5
у=-1.
4) не могу решить
