Решением данной системы является пара чисел: 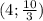 .
.
Объяснение:
Перед нами система уравнений с двумя неизвестными:
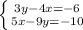
Данную систему уравнений проще решить, используя метод исключения одной переменной. Для этого домножим обе части первого уравнения на 3:
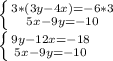
Теперь, сложим оба уравнения данной системы, чтобы избавиться от переменной y. Найдем x, путем упрощения обычного уравнения:
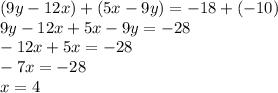
Теперь подставим данное значение в первое уравнение системы, чтобы найти y:
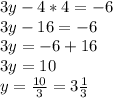
Получили ответ, что решением данной системы является пара чисел: 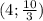
Найдем значение выражения 9 1/6 : (4 1/3 - 8) + 24 * 3/8.
Сначала в порядке очереди находим значение выражения в скобках, затем вычисляем умножение или деление, потом проводятся действия сложения или вычитания. То есть получаем:
9 1/6 : (4 1/3 - 8) + 24 * 3/8 = (9 * 6 + 1)/6 : (4 + 1/3 - 8) + 24 * 3/8 = (54 + 1)/6 : (- 4 + 1/3) + 24 * 3/8 = 55/6 : (- 3 - 3/3 + 1/3) + 3 * 8 * 3/8 = 55/6 : (- 3 - 2/3) + 3 * 1 * 3/1 = 55/6 : (- 11/3) + 3 * 3 = - 55/6 : 11/3 + 3 * 3 = - 55/6 * 3/11 + 3 * 3 = - 11 * 5/(2 * 3) * 3/11 + 9 = 5/2 + 9 = 2,5 + 9 = 11,5;
ответ: 11,5.
тогда (х - 1) : 2 км/ч - скорость пешехода.
1 час 40 мин = 5/3 часа
12/х + 5/3 = 12/((х - 1) : 2)
12/х + 5/3 = 24/(х - 1)
12 · 3 · (х - 1) + 5 · х · (х - 1) = 24 · 3 · х
36х - 36 + 5х² - 5х = 72х
31х - 36 + 5х² = 72х
5х² + 31х - 72х - 36 = 0
5х² - 41х - 36 = 0
D = (- 41)² - 4 · 5 · (- 36) = 1681 + 720 = 2401 = 49²
х₁ = (41 + 49)/(2 · 5) = 90/10 = 9 (км/ч) - скорость велосипедиста.
х₂ = (41 - 49)/(2 · 5) = - 8/10 = - 0,8 (км/ч) - не подходит.
(9 - 1) : 2 = 4 (км/ч) - скорость пешехода.
ответ: скорость велосипедиста 9 км/ч, пешехода 4 км/ч.