24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
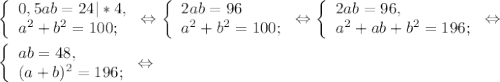

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
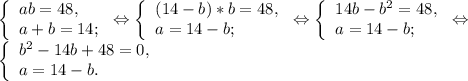
Решим квадратное уравнение:
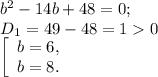
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
ответ:
x∈(-∞; -6)∪(6; 10]
объяснение:
(x^2-16x+60)/(x^2-36)≤0
y=(x^2-16x+60)/(x^2-36)
(x^2-16x+60)/(x^2-36)=0
1) x^2-16x+60=0
d=256-4*60=256-240=16
2) x^2-36≠0
x^2≠36
x≠6
x≠-6
- + - +
---()()*>
(-6) (6) 10
x∈(-∞; -6)∪(6; 10]
(х + 54) - скорость второго автомобилиста на второй половине пути
примем за 1 длину всего пути, 1/2 - половина пути, тогда
1/х - время, затраченное первым автомобилистом на весь путь
1/2 : 36 = 1/72 - время, затраченное вторым автомобилистом на первую половину пути
1/2 : (х + 54) = 1/(2(х + 54)) - время, затраченное вторым автомобилистом на вторую половину пути
Уравнение
1/х = 1/72 + 1/(2(х + 54))
72* (x + 54) = x * (x + 54) + x * 36
72x + 3888 = x² + 54x + 36x
х² + 18х - 3888 = 0
D = 18² - 4 * 1 * (- 3888) = 324 + 15552 = 15876
√D = √15876 = 126
х₁ = (- 18 + 126) /2 = 108/2 = 54 км/ч - искомая скорость первого
х₂ (-18 - 126) / 2 = - 144/2 = - 72 отрицательное значение не удовлетворяет условию