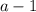 нечетное , но в то же время
нечетное , но в то же время  четное , но
четное , но 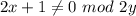 значит , это возможно когда
значит , это возможно когда 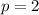 , тогда
, тогда 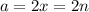
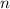 частное при делений на простое число , отсюда следует , что частное при делений
частное при делений на простое число , отсюда следует , что частное при делений  на
на 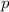 , может быть четным и нечетным числом ,и оно согласуется со вторым условием
, может быть четным и нечетным числом ,и оно согласуется со вторым условием 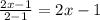 ,то есть
,то есть 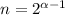 подходит,значит
подходит,значит 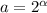 , но и походит другие числа ,содержащие множитель
, но и походит другие числа ,содержащие множитель 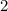
Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Я уже отвечала тебе