Обозначим скорость катера -- х км\ч, скорость течения реки---у км\ч. По течению реки скорость катера будет ( х+у) , против течения ---(х-у) , а в стоячей воде-х. Составим систему согласно условия:{4(x+y)+3x=148 {5(x-y)-2x=50{7x+4y=148 {3x-5y=50Решим систему сложения. Первое уравнение системы умножим на 5, а второе -- на 4 .35x+20y=740 + {12x-20y=20047x=940x=20 скорость катераПодставим значение х в любое уравнение системы и найдём у:( например , в первое)7·20+4у=148140+4у=1484у=148-1404у=8у=2 скорость течения рекиответ: 20 км\ч ; 2 км\ч
Данное уравнение не содержит самой неизвестной функции y(x), поэтому можно понизить порядок уравнения. Пусть y'(x)=z(x)⇒y''(x)=z'(x) и уравнение примет вид (1+4*x³)*z'=12*x²*z. Разделив обе части на 1+4*x³, получаем уравнение z'=dz/dx=12*x²*z/(1+4*x³). Умножая обе части на dx и разделив на z, приходим к уравнению dz/z=12*x²*dx/(1+4*x³). А так как d(1+4*x³)=12*x²*dx, то это уравнение можно записать в виде dz/z=d(1+4*x³)/(1+4*x³). Интегрируя обе части, получаем ln/z/=ln/1+4*x³/+lnC1, где C1>0 - произвольная постоянная. Отсюда ln/z/=ln/C1*(1+4*x³)/, z(x)=C1*(1+4*x³) и мы приходим к уравнению y'=dy/dx=C1*(1+4*x³). Умножая на dx, получаем dy=C1*(1+4*x³)*dx. Интегрируя обе части, получаем y(x)=C1*x+C1*x⁴+C2. Проверка: y'(x)=C1+4*C1*x³, y''(x)=12*C1*x², (1+4*x³)*y''-12*x²*y'=12*C1*x²*(1+4*x³)-12*x²*C1*(1+4*x³)=0 - решение найдено верно. ответ: y(x)=C1*x*(1+x³)+C2.
Из второго уравнения выразим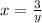
Подставим в первое уравнения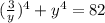
Пусть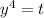
По теореме Виета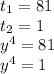
ответ (3,1), (-3,-1), (1,3), (-1,-3)