1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
Выбирай из того, что
Скорость грузового - 40, легкового - 50
за первый час легковой догонит грузового на 50-40=10 км
за второй на 10+(55-40)=25 км. и тд. каждый час все больше.
Положим, что первый член равен 10, тогда второй - 15 ,третий 20 и т.д.
Сумма членов прогрессии 10,15,20,25... должна равнятся 135
Сумма АП равна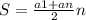 
, но т.к. последний член не известен выразим an через a1 и n: 
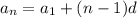и формулу суммы можно переписать в виде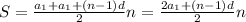 
Подставим известные данные
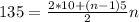
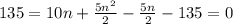
Решим квадратное уравнение
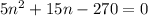
Положительный корень x = 6 показывает количество членов Ап. т.е. часов за которые легковой догонит грузового
3x² -11x-20 =0 ;
D =11² -4*3*(-20)=361 =19²⇒√D=19.
x₁ =(11-19)/(2*3) =8/(-6)= - 4/3;
x₁ =(11+19)/(2*3) =30/6 =5.
Нули функция f(x) =3x² -11x-20 Ж - 4/3 и 5 .
3x² -11x-20 < 0
f(x) <0 ;
3(x+4/3)(x-5) <0 ;.
методом интервалов:
+ - +
(-4/3) (5)
x∈ (-4/3 ;5) .
На интервале (-4/3 ;5) функция отрицательно (при исех x∈ (-4/3 ;5) f(x) <0 ).
f(x) >0 ,если x∈(-∞ ; -4/3) (5 ;∞) .
2) f(x)=6-3√2-x ; примитивно
Нули функция f(x)=6-3√2-x.
6-3√2- x=0 ;
x = 6-3√2 ;
f(x) < 0 ⇔6-3√2-x<0 ⇒x >6-√2 . f(x) < 0 , при x ∈(6-√2 ;∞).
f(x) > 0 ⇔6-3√2-x>0 ⇒x <6-√2. f(x) < 0 ,при x∈(∞; -6-√2).
наверно 2) f(x)=6-3√(2-x)
f(x)=6-3√(2-x) . ООФ: x∈(-∞;2] * * * 2-x ≥0 ⇔x ≤ 2. * * *
f(x)=0⇒6-3√(2-x)= 0⇔2= √(2-x)⇒4=2- x ⇔ x =- 2 .
f(x) <0⇔ 6-3√(2-x) <0 ⇔3√(2-x) >6 ⇔√(2-x) >2 ⇔2-x >4⇒ x< - 2 иначе x∈(-∞; -2).
f(x) > 0⇔ x∈(-2; 2).