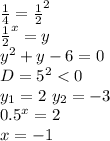
Ивану Царевичу нужно загадать 15552. Каждый день он будет делить это число на натуральное, превосходящее 1. Лучше всего делить на 2, но 2 дня подряд нельзя использовать одно и то же число, поэтому на второй день он поделит то, что получилось, на 3. На третий день снова на 2 и так далее. Чередование 2 и 3.
Делим:
15552/2=7776 (первый день);
7776/3=2592 (второй день);
2592/2=1296 (третий день);
1296/3=432 (четвёртый день);
432/2=216 (пятый день);
216/3=72 (шестой день);
72/2=36 (седьмой день);
36/3=12 (восьмой день);
12/2=6 (девятый день);
6/3=2 (десятый день);
2/2=1 (одиннадцатый день, в который его съедят).
Итак, загадав 15552, Иван Царевич сможет продержаться ещё 10 дней.
Чтобы получить это число, необходимо понимать, что в конце концов мы придём к 1. Поэтому 15552 мы получим следущий образом:
1•2•3•2•3•2•3•2•3•2•3•2 (6 умножений на 2 и 5 умножений на 3).
ответ:
задать вопрос
войти
октября 16: 24
докажите, что данное уравнение имеет целые корни и найдите их: х^(2)=(√(7−2×√(6))−√(7+2×√()
ответ или решение1
андреева анна
раскроем скобки и решим уравнение, при этом воспользуемся формулами сокращенного умножения:
(a - b)2 = a2 - 2 *a * b + b2.
(a - b)* (а + b) = a2 - b2.
(√(7 - 2 * √6) - √(7 + 2 * √6)) 2 = (√(7 - 2 * √6))2 - 2 * √(7 - 2 * √6) * √(7 + 2 * √6) + √(7 + 2 * √6))2 = 7 - 2 * √6 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) + 7 + 2 * √6 = 14 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) = 14 - 2 * √(72 - (2 * √6) 2) = 14 - 2 * √(49 - 4 * 6) = 14 - 2 * √(49 - 24) = 14 - 2 * √25 = 14 - 2 * √52 = 14 - 2 * 5 = 14 - 10 = 4.
следовательно:
х2 = 4.
х = √4.
х1 = 2; х2 = -2.
ответ: уравнение х2 = (√(7 - 2 * √6) - √(7 + 2 * √6)) 2 имеет корни х1 = 2; х2 = -2
объяснение: