Точки с координатами (-2;8) и (1;5)
Объяснение:
Первая функция
у= х²+4 (1)
Выразим у во второй функции:
х+у = 6 <=> у = 6-х (2)
Точка пересечения - точка, с некими координатами (х0;у0), которые принадлежат обоим графикам функций.
То есть нам надо найти такие х и у, для которых верно равенство 1 и 2.
Приравняем у в (1) и (2) функциях. Получим:
у = х²+4 = 6-х
Или

Найдем у для х=(-2) и х=1
Для этого подставим значение х в любую из 2х функций
При х = (-2)
у(-2) = 6-(-2) = 6+2 = 8
Следовательно одна из искомых точек имеет координаты:
(-2;8)
При х=1
у(1) = 6-1 = 5
Следовательно вьорая искомая точек имеет координаты:
(1;5)
ответ: (-2;8) и (1;5)
Обе функции монотонно возрастающие.
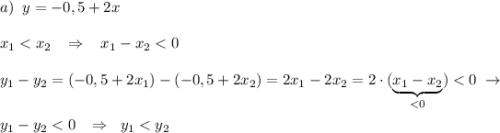
Получили, что мЕньшему значению переменной соответствует мЕньшее значение функции, и наоборот, бОльшему значению переменной соответствует бОльшее значение функции. Значит функция возрастающая .
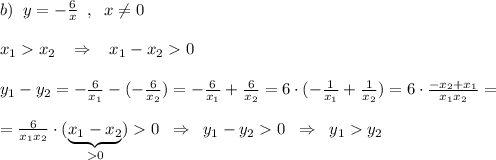
Знак выражения получили (+) , так как произведение 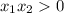 в силу того, что гиперболу рассматриваем на двух промежутках при
в силу того, что гиперболу рассматриваем на двух промежутках при 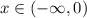 и при
и при 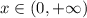 , где
, где 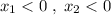 и
и 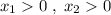 .
.
Получили, что бОльшему значению переменной соответствует бОльшему значение функции, и наоборот, мЕньшему значению переменной соответствует мЕньшему значение функции. Значит функция возрастающая .
4x^2-20х+25=(2х-5)^2.