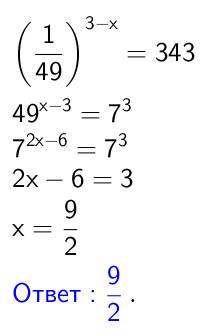
Для исследования функции сначала нужно взять производную. Чтобы проще было взять воспользуемся формулой сложения степеней: 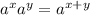
Получим что: 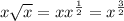
Теперь перепишем функцию:
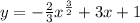
И берем производную:
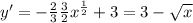
Дальше найдем точку где производная обращается в 0.
Для этого решаем уравнение: 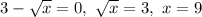
Это будет точка экстремума. Но точка экстремума может быть как минимумом так и максимумом. Надо показать что это максимум. Как это делается. Есть 2 метода.
1 метод:
Рассмотрим как ведет себя производная при x<9 и при x>9. Очевидно, что при x>9 производная 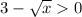 . Значит функция растет. При x>9, наоборот
. Значит функция растет. При x>9, наоборот ![3-\sqrt{x}<0[/tex]. Значит функция убывает. Если до точки х=9 функция растет, а после нее убывает, то получается что это максимум функции</p <p </p <p2 метод:</p <pВозьмем вторую производную от исходной функции получим [tex]y''=-\frac{1}{2\sqrt{x}}](/tpl/images/0065/6514/3770b.png) . Для любых положительных х, вторая производная будет меньше нуля, т.е y''<0. Это необходимое и достаточное условие, чтобы функция была выпуклой вверх. Т.к. функция выпулкая вверх, то точка экстремума будет точкой максимума. ч.т.д
. Для любых положительных х, вторая производная будет меньше нуля, т.е y''<0. Это необходимое и достаточное условие, чтобы функция была выпуклой вверх. Т.к. функция выпулкая вверх, то точка экстремума будет точкой максимума. ч.т.д
ответ: точка максимума x=9, значение функции в этой точке y(9)=10
1. Цветных шаров в ящике 5, поэтому вероятность вытащить цветной шар равна  , что равно 0,5.
, что равно 0,5.
ответ: вероятность того, что вынутый наугад шар цветной равна 0,5.
2. Еще раз напишу условие, для удобста: cos 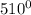 - sin
- sin 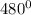 + tg
+ tg 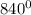 .
.
Рассмотрим каждое слагаемое в отдельности:
cos 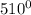 = cos
= cos 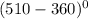 = cos
= cos 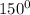 = -
= - 
sin 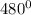 = sin
= sin 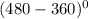 = sin
= sin 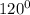 =
= 
tg 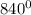 = tg
= tg 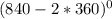 = tg
= tg 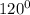 = -
= - 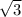
Теперь заменим слагаемые в исходном выражении полученными значениями:
cos 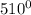 - sin
- sin 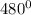 + tg
+ tg 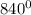 = -
= -  -
-  -
- 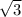 = -2*
= -2*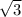
ответ: -2*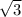
3. В физике уравнение движения точки выглядит следующим образом:
S = 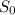 +
+ 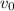 t +
t + 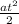
Обратимся теперь к уравнению, данному в условии:
S(t) = 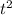 - 8t + 4
- 8t + 4
Заметим, что 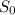 = 4,
= 4, 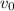 = -8, a = 2.
= -8, a = 2.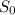
Уравнение изменения скорости:
v = 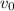 + at
+ at
Подставим в него вместо v - 0, как требуется в условии и вместо 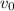 и a найденные нами значения и решим полученное уравнение:
и a найденные нами значения и решим полученное уравнение:
0 = -8 + 2t
8 = 2t
t = 4
ответ: скорость точки окажется равной нулю через 4 единицы времени после начала движения.
4. Формула объема правильного тетраэдра:
V = 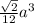 , где a - длина ребра.
, где a - длина ребра.
Пусть ребро данного тетраэдра равно l. Тогда его объем выражается формулой 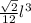 , обозначим его как
, обозначим его как 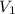 .
.
Ребро же нового тетраэдра равно 4l.
Подставим его в формулу объема, вместо a:
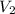 =
= 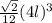 =
= 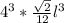 =
=  = 64
= 64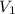
Подставим вместо 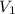 значение, данное в условии:
значение, данное в условии:
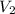 = 64*3 = 192 см
= 64*3 = 192 см
ответ: объем такого правильного тетраэдра равен 192 см