Ноль функции, это такое значение аргумента функции при котором функция обращается в ноль.
A) y=2,1·x-70; y - функция; x - аргумент функции.
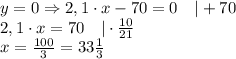
Как видно функция имеет ноль, х=33 целых и 1/3
B) y=4x·(x-2)
y=0 ⇒ 4x·(x-2)=0
Произведение равно нулю, когда один из множителей равен нулю и всё выражение существует. То есть
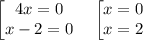
Эта функция имеет даже два нуля, х={0;2}.
Дана точка А(-2;7), значит ее абсцисса равна -2, ее ордината равна 7
1) Ордината точки A меньше её абсциссы - Неверно, ордината точки А больше абсциссы.
2) Точка A лежит в третьей координатной четверти - Неверно, в третьей координатной четверти абсцисса и ордината отрицательны, у точки А ордината положительна.
3) Точка A находится в нижней полуплоскости - Неверно, в нижней полуплоскости ордината отрицательна, у точки А ордината положительна.
4) Точка A находится в левой полуплоскости - Верно, в левой полуплоскости абсцисса отрицательна.
5) Точка A лежит на оси ординат - Неверно, на оси ординат абсцисса равна нулю, у точки А абсцисса не равна нулю.
ответ: Точка A находится в левой полуплоскости
1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=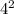 =16 б)у(-3)=
=16 б)у(-3)=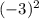 =9 в) у(2)=
=9 в) у(2)=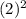 =4
=4
у(3)=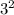 =9 у(-2)=
=9 у(-2)=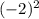 =4 у(-5)=
=4 у(-5)=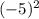 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Нули функции : f(x) = 0
A) y = 2,1x - 70; 2,1x - 70 = 0
Ноль линейной функции в точке x = 33,(3)
B) y = 4x(x - 2); 4x(x - 2) = 0
Квадратичная функция имеет два нуля : x₁ = 0; x₂ = 2