Объяснение:
1. Функция задана формулой y = -2x + 7.
Определите:
1) значение функции, если значение аргумента равно 6;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=6
у= -2*6+7= -5 при х=6 у= -5
2) значение аргумента, при котором значение функции равно -9;
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
-9= -2х+7
2х=7+9
2х=16
х=8 у= -9 при х=8
3) проходит ли график функции через точку А(-4;15).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
15= -2*(-4)+7
15=15, проходит.
2. Постройте график функции y = 3x – 2.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -5 -2 1
Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 2;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=2
у=3*2-2=4 у=4 при х=2
Согласно графика, также при х=2 у=4
2)значение аргумента, при котором значение функции равно -5.
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
y = 3x – 2
у= -5
-5=3х-2
-3х= -2+5
-3х=3
х= -1 у= -5 при х== -1
Согласно графика, у= -5 при х= -1.
3. Не выполняя построения, найдите координаты точек пересечения графика функции у = 0,5х - 3 с осями координат.
а)график пересекает ось Ох при у=0:
у=0
0=0,5х-3
-0,5х= -3
х= -3/-0,5
х=6
Координаты точки пересечения графиком оси Ох (6: 0)
б)график пересекает ось Оу при х=0:
х=0
у=0-3
у= -3
Координаты точки пересечения графиком оси Оу (0; -3)
4. При каком значении к график функции у = kx- 6 проходит через точку А (-2; 20)?
х= -2
у=20
20=k*(-2)-6
20= -2k-6
2k= -6-20
2k=-26
k= -13
Уравнение: у= -13х-6
5. Постройте график функции:
y (-2х, если х 2, -4, если х > 2.
Неясное задание.
8
Объяснение:
Сложим два равенства, получим уравнение:
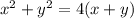
Раскроем скобки справа, перенесем влево и дополним до полных квадратов относительно х и у:
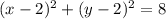
Выражаем x через y:
(вообще, правильнее было бы рассмотреть два случая: когда перед корнем стоит знак плюс, что мы и делаем, и когда перед ним стоит знак минус, но нас интересует максимальное значение, логичнее было бы рассмотреть только положительное значение)
Наша целевая функция, в которой будем находить максимум, имеет вид:
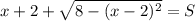, где S - сумма решений системы уравнений.
Найдем производную по х, приравняем к нулю эту функцию
Получим
Таким образом, мы сможем найти y: y₁ = 4; y₂ = 4
Стало быть, только в точке (4;4) достигается этот максимум суммы, которая равна 4+4 = 8
одз;
х - не равно pi/2+pi*к и 3х - не равно pi/2+pi*к
tgx-tg 3x=0
(sin(x)*cos(3x)-sin(3x)*cos(x)) / (cos(x)*cos(3x))=0
(sin(x)*cos(3x)-sin(3x)*cos(x))=0
sin(x-3х)=0
sin(2х)=0
2х=pi*к
х=pi/2*к
ответ с учетом ОДЗ х=pi*к
cos2x+sin(3pi/2-x)=0
cos2x-cos(x)=0
-2*sin(x/2)*sin(3x/2)=0
x/2=pi*k или 3x/2=pi*k
x=2pi*k или x=2pi*k/3
ответ x=2pi*k/3
sin2x=cosx
sin2x=cosx
2sin(x)*cos(x)-cosx=0
(2sin(x)-1)*cos(x)=0
sin(x)=1/2 или cos(x)=0
х = (+/-)pi/6+2*pi*k или х=pi/2+pi*k - это ответ