1. Обратно пропорциональная зависимость :
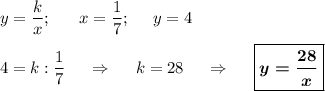
2. Решите графически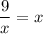 
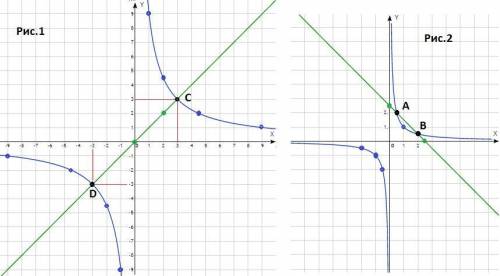
График функции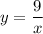 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции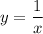 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
1)а) x²+3x-4=0
Коэффициенты: старший = 1
Второй = 3
Свободный член = -4
б)x²+14x=0
Коэффициенты: старший = 1
Второй = 14
Свободный член = 0
2) а)x² -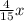 
+ 
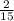=0
б)x² - 3x - 12 = 0
3) а) 0; -5
б) -3 ; 3
в) √5,5 ; -√5,5
Объяснение:
1)
a. (x-1)(x+4)=0
x²+4x-x-4=0
x²+3x-4=0
Коэффициенты: старший = a = 1
Второй = b = 3
Свободный член = c = -4
b. 12 - 6(x+3) -7x = (x-2)(x+3)
12 - 6x - 18 - 7x = x²+3x-2x-6
-6-13x = x²+x-6
-6-13x -x²-x+6=0
-x²-14x=0 (домножили на -1)
x²+14x=0
Коэффициенты: старший = a = 1
Второй = b = 14
Свободный член = c = 0
2.
a) -15x²+4x-2=0 разделим на -15
x² - 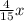+ 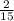=0
б) 12 - x² + 3x = 0
- x² + 3x+12=0 домножим на -1
x² - 3x - 12 = 0
3.
a) x²+5x =0
x(x+5) =0
Произведение равно 0, когда один из множителей равен 0
x1=0 или x+5=0
x2= -5
б) x² - 9 =0
x²=9
x1 = √9 = 3
x2 = -√9 = -3
в) -2x²+11=0
-2x²=-11 разделим на -2
x² = 5,5
x1=√5,5
x2= -√5,5
Если сумма чисел от 1 до 28 должна быть 203, то она складывается из ряда чисел от 1 до 7 и 22 до 28 или из чисел от 8 до 21, однако брать все числа подряд невозможно, поскольку в них много пар, которые в сумме дают 29. Причем 29 складывается всегда из одного четного и одного нечетного числа. Поэтому целесообразно рассмотреть отдельно ряд четных и ряд нечетных чисел от 1 до 28.
Нечетные 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27 (сумма чисел 196)
Чётные 28, 26, 24, 22, 20, 18, 16, 14, 12, 10, 8, 6, 4, 2 (сумма 210)
Пишу наглядно, чтобы было видно пары четных и нечетных, которые в сумме (по вертикали) составляют 29.
У нечетных не хватает до суммы 203 числа 7, у четных - 7 единиц лишних. Можно заменить у нечетных 11 на 18 (разница как раз 7), либо у четных 18 на 11, тогда сумма чисел в ряду будет 203.
Сумма квадратов у ряда нечетных, с учетом замены 11 на 18, будет 3857.
Сумма квадратов у ряда четных, с учетом замены 18 на 11, будет тоже 3857.
Поэтому можно принять любое решение:
либо это ряд 1,3,5,7,9,13,15,17,18,19,21,23,25,27;
либо это ряд чисел 2,4,6,8,10,11, 12,14,16,20,22,24,26,28,
сумма квадратов будет наименьшей и составлять 3857.