y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.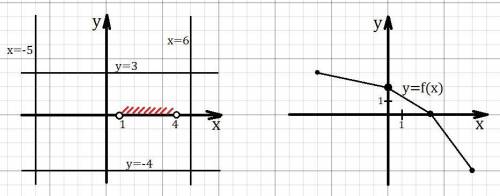
Если одночлены состоят из одинаковых переменных в одинаковых степенях, то они являютсяподобными. Коэффициенты одночленов при этом могут различаться. Примеры подобных одночленов:
3a2 и –4a2; 31 и 45; a2bx4 и 1,4a2bx4; 100y3и 100y3
Но одночлены –6ab2 и 6ab не являются подобными, так как у них переменная b находится в разных степенях.
Подобные одночлены обладают удивительным свойством — их можно легко складывать и вычитать. Если нужно найти сумму двух или более подобных одночленов, то их коэффициенты надо сложить, а переменные в сумме оставить без изменений. Если же требуется найти разность двух подобных одночленов, то коэффициент одного одночлена надо вычесть из второго, а переменные оставить без изменений. Примеры:
4x2 + 15x2 = 19x2
5ab – 1,7ab = 3,3ab
13a10b5c3 – 13a10b5c3 = 0a10b5c3 = 0
Эти действия называются приведением подобных одночленов.
Почему же подобные одночлены можно так складывать и вычитать? Попробуем упростить выражения, не используя правила приведения подобных одночленов:
2x + 4x = (x + x) + (x + x + x + x) = x + x + x + x + x + x = 6 * x = 6x
2x – 4x = (x + x) – (x + x + x + x) = x + x – x – x – x – x = – x – x = – (x + x) = –(2x) = –2x
То есть свойство подобных членов вытекает из правила арифметики о том, что произведение двух чисел является ничем иным как суммой из слагаемых одного числа, где количество слагаемых равно другому числу:
2 * 3 = 3 + 3 = 2 + 2 + 2
решить показательное уравнение
2^sin^2x + 4*2^cos^2x=6
2^sin²x + 4*2^(1 - sin²x) = 6
2^sin²x + 4*2* 2^( - sin²x) = 6
2^sin²x + 8 / 2^(sin²x) = 6 умножим на 2^sin²x
(2^sin²x)² - 6* (2^sin²x) + 8 = 0
пусть 2^sin²x = t
t² - 6t + 8 = 0
t1 = 2
t2 = 4
2^sin²x = 2
1) sin²x = 1
а) sinx = - 1
x1 = - π/2 + 2πk, k∈z
б) sinx = 1
x2 = π/2 + 2πn, n∈Z
2) 2^sin²x = 4
2^sin²x = 2²
sin²x = 2
в) sinx = - √2
x3 = (-1)^(n + 1)*arcsin(√2) + πm, m ∈Z
г) sinx = √2
x4 = (-1)^(n)*arcsin(√2) + πs, s ∈Z