А.
любое число со знаком минус во второй степени принимает положительное значение
например:
(-4)^2=16
(-5)^2=25
Б.
любое число со знаком плюс во второй степени принимает положительное значение
например:
2^2=4
3^2=9
В.
если к любому числу со знаком плюс во 2 степени прибавить любое число, то выражение будет принимать положительное значение
например:
2^2+2=6
3^2+2=11
Г.
(x + 2)^2
если к любому числу со знаком плюс прибавить любое число и возвести в квадрат то выражение будет принимать положительное значение.
например:
(2+2)^2=16
(3+3)^2=36
Периметр фигуры – сумма длин всех её сторон. Площадь фигуры – произведение её сторон. Запишем периметр квадрата по формуле:
х + х + х + х = 4х, где х – сторона квадрата.
Тогда его площадь:
х × х = х²
Теперь, допустим, что периметр квадрата увеличился в 6 раз:
4х × 6 = 24х
Тогда, каждая его сторона:
24х : 4 = 6х
Как видим, каждая сторона увеличилась в 6 раз.
Теперь, высчитаем площадь:
6х × 6 = 36х²
Сравним новую площадь со старой:
36х² : х² = 36
Как видим, площадь квадрата увеличилась в 36 раз.
ответ: в 36 раз.
Объяснение:
Пусть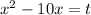 . Тогда уравнение принимает вид:
. Тогда уравнение принимает вид:
Тогда получим
Покажем решение квадратных уравнений отдельно.