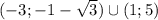Пусть в сектор  вписан прямоугольник
вписан прямоугольник  .
.  и
и  - середины сторон
- середины сторон  и
и  соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
Так как прямоугольник симметричен оси симметрии сектора, то:
Проведем луч 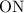 , составляющий с осью симметрии сектора угол
, составляющий с осью симметрии сектора угол  . Зададим ограничения на х:
. Зададим ограничения на х: ![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png)
Найдем сторону прямоугольника, перпендикулярную оси симметрии сектора.
Рассмотрим треугольник  . Запишем соотношение для синуса угла х:
. Запишем соотношение для синуса угла х:
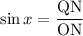
Заметим, что 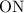 соответствует радиусу сектора. Тогда, выражение для
соответствует радиусу сектора. Тогда, выражение для 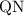 примет вид:
примет вид:

Так как 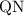 - половина стороны
- половина стороны  , то найдена первая сторона прямоугольника:
, то найдена первая сторона прямоугольника:

Найдем сторону прямоугольника, параллельную оси симметрии сектора. Представим ее длину в виде:
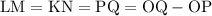
Длину найдем из того же прямоугольного треугольника  , записав выражение для косинуса угла
, записав выражение для косинуса угла  :
:

Выражаем  :
:
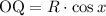
Длину  найдем из прямоугольного треугольника
найдем из прямоугольного треугольника 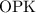 . Запишем выражение для тангенса угла
. Запишем выражение для тангенса угла  :
:

Откуда:

Так как 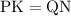 , то:
, то:
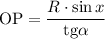
Таким образом, найдена вторая сторона прямоугольника:

Площадь прямоугольника равна произведению его смежных сторон:


Найдем производную:
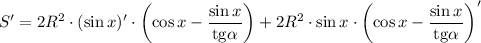

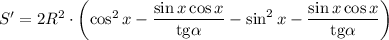
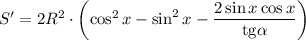
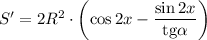
Приравняем производную к нулю:
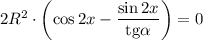
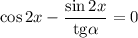
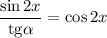
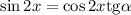
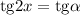
Учитывая ограничения ![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png) получим, что:
получим, что:
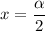
Проверим, является ли эта точка точкой экстремума.
Найдем значение производной при 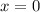 :
:

Найдем значение производной при  :
:
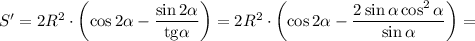
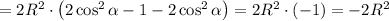
При переходе через точку 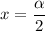 производная меняет знак с плюса на минус. Значит, это точка максимума.
производная меняет знак с плюса на минус. Значит, это точка максимума.
Найдем значение максимума:


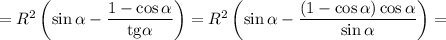

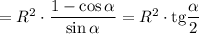
Значит, наибольшая площадь прямоугольника равна 
ответ: 

ОДЗ:
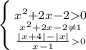
Решаем каждое неравенство:
 ⇒
⇒ 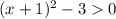 ⇒
⇒

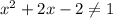 ⇒
⇒  ⇒
⇒ 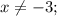
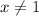

Подмодульные выражения обращаются в 0 в точках
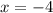 и
и 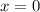
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
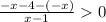 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
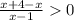 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 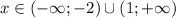
ОДЗ:

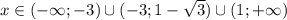
Решаем неравенство: 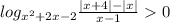
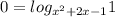
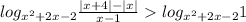
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
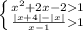 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
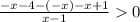 ⇒
⇒  ⇒
⇒ 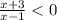 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
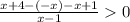 ⇒
⇒ 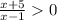 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 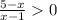 ⇒
⇒ 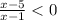 ⇒
⇒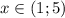
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
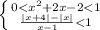 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
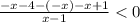 ⇒
⇒ 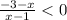 ⇒
⇒ 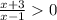 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
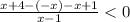 ⇒
⇒ 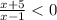 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 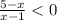 ⇒
⇒ 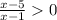 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: