Алгебра: Сколько корней имеет уравнение: -3х^2+7х-4=0

Сколько корней имеет уравнение: -3х^2+7х-4=0

👇

Увидеть ответ

Ответ:

Imdoingfinetoday123

07.07.2021

D=49-48=1,так как дискриминант больше нуля,уравненные имеет два корня

4,6(20 оценок)

Открыть все ответы

Ответ:

санёк1234567817626

07.07.2021

Рассмотрим сначала числа со старшим разрядом единиц
(в обратном порядке):

$9^2 = 81 \ ;$        сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа.

$4^2 = 16 \ ;$        искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.

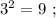$3^2 = 9 \ ;$        искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.

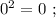$0^2 = 0 \ ;$        искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.

Теперь переходим к старшему разряду десятков
(в обратном порядке):

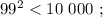$99^2 < 10 \ 000 \ ;$        сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.

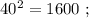$40^2 = 1600 \ ;$        сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.

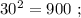$30^2 = 900 \ ;$        сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 .

$10^2 = 100 \ ;$        сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 .

Далее переходим к старшему разряду сотен
(в обратном порядке):

$999^2 < 1 \ 000 \ 000 \ ;$        сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.

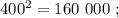$400^2 = 160 \ 000 \ ;$        сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.

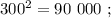$300^2 = 90 \ 000 \ ;$        сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .

$100^2 = 10 \ 000 \ ;$        сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .

Ну и ещё переходим к старшему разряду тысяч
(в обратном порядке):

$9 \ 999^2 < 100 \ 000 \ 000 \ ;$        сумма: 4 + 8 = 12 , у квадрата вдвое больше.

$4000^2 = 16 \ 000 000 \ ;$        сумма: 4 + 8 = 12 , у квадрата вдвое больше.

$3000^2 = 9 \ 000 000 \ ;$        сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .

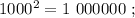$1000^2 = 1 \ 000 000 \ ;$        сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .

А теперь всё обобщим на самый общий случай.

Если бы число записывалось единицей с R нолями, то его квадрат содержал бы уже 2R нолей, при этом в исходном числе было бы (R+1) цифр, а в квадрате числа – (2R+1) цифр.

Пусть у нас старший разряд таков, что во всём числе только R цифр, рассмотрим всё, как обычно в обратном порядке:

( 99999 : : : R цифр : : : 99999 )   –   это число на единицу меньше, чем число     ( 100000 : : : R нулей : : : 00000 )     , в котором (R+1) цифр.

квадрат числа [( 99999 : : : R цифр : : : 99999 )]    –   это число, меньшее, чем число     ( 100000 : : : 2R нулей : : : 00000 )     , в котором (2R+1) цифр.

Значит, квадрат числа ( 99999 : : : R цифр : : : 99999 ) содержит ровно 2R цифр, а всего само число и его квадрат содержат 3R цифр.

в числе ( 400000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 400000 : : : (R–1) нулей : : : 00000 )] =
= ( 1600000 : : : (2R–2) нулей : : : 00000 ) содержит 2R цифр, а всего само число и его квадрат содержат 3R цифр.

в числе ( 300000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 300000 : : : (R–1) нулей : : : 00000 )] =
= ( 900000 : : : (2R–2) нулей : : : 00000 ) содержит (2R–1) цифр, а всего само число и его квадрат содержат (3R–1) цифр.

в числе ( 100000 : : : (R–1) нулей : : : 00000 ) содержится R цифр.

квадрат числа [( 100000 : : : (R–1) нулей : : : 00000 )] =
= ( 100000 : : : (2R–2) нулей : : : 00000 ) содержит (2R–1) цифр, а всего само число и его квадрат содержат (3R–1) цифр.

И так будет для любого R

R = 1   : : : сумма: 3R = 3 или (3R–1) = 2 .
R = 2   : : : сумма: 3R = 6 или (3R–1) = 5 .
R = 3   : : : сумма: 3R = 9 или (3R–1) = 8 .
R = 4   : : : сумма: 3R = 12 или (3R–1) = 11 .
R = 5   : : : сумма: 3R = 15 или (3R–1) = 14 .

. . .

R = 32   : : : сумма: 3R = 96 или (3R–1) = 95 .
R = 33   : : : сумма: 3R = 99 или (3R–1) = 98 .
R = 34   : : : сумма: 3R = 102 или (3R–1) = 101 .
R = 35   : : : сумма: 3R = 105 или (3R–1) = 104 .

... и т.д и т.п. ...

Как легко видеть, в этой последовательности:

2, 3, 5, 6, 8, 9, 11, 12, 14, 15 .... 95, 96, 98, 99, 101, 102, 104, 105 ....

пропущены определённые числа. Пропущенные числа:

1, 4, 7, 10, 13, 16 .... 94, 97, 100, 103, 106 ....

подчиняются закону (3R+1).

В самом деле, между предыдущим и последующим значениями, кратными трём, всегда содержатся два целые числа, а искомой суммой, помимо 3R, может быть только одно из них: (3R–1) .

Поэтому, значения, подчиняющиеся закону (3R+1) не могут быть искомым результатом. Так, например, число 99 – кратно трём ( 99 = 3*33 ), а значит, число   100 = 3*33+1   никак не могло бы оказаться в расчётах Лены.

О т в е т : у Лены не могли получиться результаты, подчиняющиеся закону (3R+1) , где R – какое угодно целое число.

ну и, конечно, все результаты Лены могут быть только положительными, поскольку это количества, т.е. натуральные величины.

в частности, у неё не могло получиться число 100.

4,5(8 оценок)

Ответ:

machismo

07.07.2021

Допустим, что у нас есть все числа от 20 до 49 в ряд. как проверить будет делиться это число на 11 или нет. по признаку: нужно сложить числа на четных местах и затем на нечетных, вычесть из одного числа другое и если получиться число, которое делиться на 11 или ноль, то исходное число будет делиться на 11. Так и сделаем.
Так как мы записывали подряд двузначные числа, но на нечетных буду стоять десятки этих чисел, а на нечетных - единицы.
значит на нечетных общая сумма будет: 2·10+3·10+4·10=90
а на четных: 3·(0+1+2+3+4+5+6+7+8+9)=3·45=135
находим разность 135-90=45 это число на 11 не делиться. Находим ближайшее к нему (так как спрашивается минимальное!! отсутствующее число) это будет 44. Значит нам нужно уменьшить разность на единицу. Так как у нас двузначные числа, то нужно, что бы разность между единицами и десятками в отсутствующем числе была 1, а минимальным таким числом будет 23.
И так, если его не будет у нас
на нечетных общая сумма будет: 2·9+3·10+4·10=88
а на четных: 3·(0+1+2+4+5+6+7+8+9)+2·3=132
тогда разность: 132-88=44 а оно делиться на 11.
ответ: 23 НАЗДОРОВЬЕ)

4,4(97 оценок)

Это интересно:

Стиль-и-уход-за-собой

27.05.2021

Как предотвратить врастание волос после эпиляции...

Кулинария-и-гостеприимство

28.09.2021

Шаг за шагом: Как пользоваться штопором и открыть бутылку вина...

Компьютеры-и-электроника

09.10.2022

Как сделать стекло в игре Minecraft: подробный гайд...

Здоровье