Выражение: (Y^4-Y^2+1)*(Y^2+1)+(Y-1)*(Y+1)
ответ: Y^6+Y^2
Решаем по действиям:
1. (Y^4-Y^2+1)*(Y^2+1)=Y^6+1
(Y^4-Y^2+1)*(Y^2+1)=Y^4*Y^2+Y^4*1-Y^2*Y^2-Y^2*1+1*Y^2+1*1
1.1. Y^4*Y^2=Y^6
Y^4*Y^2=Y^(4+2)
1.1.1. 4+2=6
+4
_2_
6
1.2. Y^2*Y^2=Y^4
Y^2*Y^2=Y^(2+2)
1.2.1. 2+2=4
+2
_2_
4
1.3. Y^4-Y^4=0
1.4. -Y^2+Y^2=0
2. (Y-1)*(Y+1)=Y^2-1
(Y-1)*(Y+1)=Y*Y+Y*1-1*Y-1*1
2.1. Y*Y=Y^2
Y*Y=Y^(1+1)
2.1.1. 1+1=2
+1
_1_
2
2.2. Y-Y=0
3. 1-1=0
-1
_1_
0
Решаем по шагам:
1. Y^6+1+(Y-1)*(Y+1)
1.1. (Y^4-Y^2+1)*(Y^2+1)=Y^6+1
(Y^4-Y^2+1)*(Y^2+1)=Y^4*Y^2+Y^4*1-Y^2*Y^2-Y^2*1+1*Y^2+1*1
1.1.1. Y^4*Y^2=Y^6
Y^4*Y^2=Y^(4+2)
1.1.1.1. 4+2=6
+4
_2_
6
1.1.2. Y^2*Y^2=Y^4
Y^2*Y^2=Y^(2+2)
1.1.2.1. 2+2=4
+2
_2_
4
1.1.3. Y^4-Y^4=0
1.1.4. -Y^2+Y^2=0
2. Y^6+1+Y^2-1
2.1. (Y-1)*(Y+1)=Y^2-1
(Y-1)*(Y+1)=Y*Y+Y*1-1*Y-1*1
2.1.1. Y*Y=Y^2
Y*Y=Y^(1+1)
2.1.1.1. 1+1=2
+1
_1_
2
2.1.2. Y-Y=0
3. Y^6+Y^2
3.1. 1-1=0
-1
_1_
0
Тоесть 2
Во всех пунктах у нас имеется n = 6*6 = 36 исходов.
a) Исходов содержащих единицу у нас m = 11:
(1,1)
(1,2),(2,1)
(1,3),(3,1)
(1,4),(4,1)
(1,5),(5,1)
(1,6),(6,1)
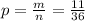
b) Т.е. сумма 2 или 3 (1 быть не может). Всего три положительных исхода:
(1,1), (1,2), (2,1). m = 3
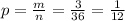
c) 11 = 6+5, 11 = 5+6, 12 = 6+6, m = 3
p(сумма чисел меньше 11) = 1 - p(сумма чисел больше или равна 11)
p(сумма чисел больше или равна 11) 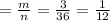
p(сумма чисел меньше 11) 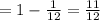
d)
p(произведение чисел меньше 27) = 1 - p(произведение чисел больше или равно 27)
6*6 = 36
6*5 = 5*6 = 30
5*5 = 25, 6*4 = 24 - не подходят. m = 3
p(произведение чисел больше или равно 27) 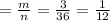
p(произведение чисел меньше 27) 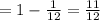
10 * х - количество атласов, 15 * у - количество контурных карт.
Составим систему уравнений и решим её методом подстановки
х + у = 15
10х = 15у
х = 15 - у Подставим значение х во второе уравнение системы
10 * (15 - у) = 15у
150 - 10у = 15у
150 = 15у + 10у
150 = 25у
у = 150 : 25
у = 6 пачек с контурными картами
х = 15 - 6 = 9 пачек с атласами
10х = 15у
10 * 9 = 15 * 6
90 = 90
ответ: 90 атласов было в библиотеке.