Объяснение:
1) log₂(x-1)=1
используем определение логарифма -
логарифмом числа b по основанию a ( logₐb ) называется такое число n, что b=aⁿ, у нас а =2, b = (x-1), n = 1 подставим наши значения
(х-1)=2¹ ⇒ х-1=2⇒х=3 отрезок (0;3]
2) log₂(x-1)≤0
по определению логарифма b >0, у нас х-1 > 0 ⇒ х > 1 это первое условие
ищем второе. сначала решаем уравнение log₂(x-1)=0
используем свойство логарифма logₐ1=0 имеем х-1 = 1 ⇒ х=2
на отрезке (1;2] проверим знак логарифма
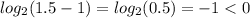
это наш отрезок (1;2]
3)
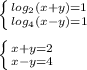
x=3; y=-1
4)
log₂(4-x)≤1
4-x>1 ⇒ x < 4
log₂(4-x)=1 ⇒ 2=4-x ⇒x=2
[2;4)
5)
log₇log₂log₇49
раскручиваем справа
log₇log₂log₇49=log₇log₂2=log₇1=0
log₁₂3+log₁₂4= log₁₂3*4=log₁₂12=1
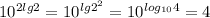
номер 4.
a)x⁴-y⁴=(x²)²-(y²)²=(x²-y²)(x²+y²)=(x-y)(x+y)(x²-y²)
Б)81-m⁴=(3²)²-(m²)²=(3²-m²)(3²+m²)=(3-m)(3+m)(3²-m²)
в)a-a⁵=-a(a-1)(a+1)(a²+1)
г)3x⁵-5x=x(3x⁴-5x)=x((3x²)²-5x)
д)2a⁴b-2b⁵=2b(a-b)(a+b)(a²+b²)
Е)3a⁵b-3ab⁵=3ab(a-b)(a+b)(a²+b²)
Задание 5
a)5m²-10mn+5n²=5(m²-2mn+n²)=5(m-n)²=5(m-n)(m-n)
б)20p-50-2p=-2(p-5)²=-2(p-5)(p-5)
в)-9x²-6x-1=-(3x+1)²
Задание 6
a)15a+10b-5ab-30=-5(a-2)(b-3)
b)75+15n-12mn-60m=3(-1)(4m-5)(n+5)
в)-30k+30-10p+10kp=10(k-p)(p-3)
Задание 7
a)16m²+2m=2m(8m-1)
b)3k-81k⁴=3k(1-27k³)
в)a⁶-a⁴b²+a³b³-ab⁵=a(a⁵-a³b²+a²b³-b⁵)=a(a-b)(a+b)²(a²-ab+b²)
г)a²b-a³b³-a²b⁴+b⁶=-b(a³b²+a²b³-a²-b⁵)
a)(x²+y²)²-4x²y²=(x-y)²(x+y)²
б)4a²b²-(a²+b²)²=-(a-b)²(a+b)²
NH судя по углу 1 и 2 биссектрисса но NH- высота так как угол при Н прямоугольный только у одного треугольника высота и бисектирсса в одниом лице а это равнобедренный соответственно MNK РАВНОБЕДРЕННЫЙ