В решении.
Объяснение:
Знайдіть усі точки графіка функції y=x2−5x+3 , у яких абсциса та ордината є протилежними числами.
Найдите все точки графика функции y=x² - 5x + 3 , в которых абсцисса и ордината являются противоположными числами.
Дана функция у = х² - 5х + 3.
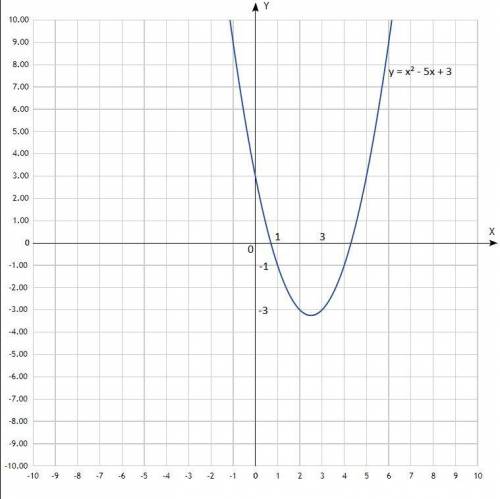
Построить график. График - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5 6 7 8
у 27 17 9 3 -1 -3 -3 -1 3 9 17 27
Согласно таблицы и графика существует две точки с указанными значениями х и у:
координаты: (1; -1); (3; -3).
18) . Всего 10 цифр: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .
Первую цифру, отличную от 0, можно выбрать , это цифры 1 , 2, ... , 9 .
Теперь для выбора второй цифры осталось 9 цифр, это цифры
0 , 1 , ... , 9 . И соответственно вторую цифру можно выбрать .
Третью цифру можно выбрать , четвёртую цифру , пятую цифру , шестую цифру , седьмую цифру .
По правилу произведения семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична от 0 , существует 9*9*8*7*6*5*4 = 544320 .
х1 + х2 = 2, или 3х1 + 3х2 = 6
х1*х2 = -d.
При условии, что 3х1 + 5х2 = 0, получаем: 5х2 - 3х2 = 0 - 6, х2 = -6/2 = -3.
Тогда х1 = 2 - (-3) = 5, х1*х2 = -3*5 = -15, и, наконец, -d = -15, d = 15.
ответ: d = 15