1)область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=5(-х)²+1=5х²+1=y(x) - значить дана функція парна за означенням парної функції
2) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=(-х)⁵+3(-х)³-(-х)=-х⁵-3х³+х=-(х⁵+3х³-х)=-y(x) значить дана функція непарна за означенням непарної функції
3) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=2*1⁴-1³+1=2-1+1=2
y(-1)=2*(-1)⁴-(-1)³+1=2+1+1=4
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна
4) область визначення множина дійсних чисел, за виключенням точки 0 (симетрична відносно початку координат)
y(-x)=3(-х)-2/(-х)=-3x+2/x=-(3x-2/x)=-y(x) значить дана функція непарна за означенням непарної функції
5) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=4*1²+[1]=4+1=5
y(-1)=4(-1)²+[-1]=4-1=3
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна
функция 
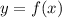не существует. То есть найдем такие значения , при которых выражение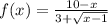 
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
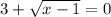, однако понятно, что 
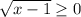, значит знаменатель не обратиться в нуль.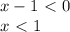
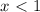функции не существует. То есть она идет от 
и куда-то дальше. Куда — нам пока неизвестно. . Может быть она периодична?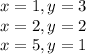 
, при котором числитель обратиться в нуль.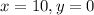 
повставлять разные значения (большие и маленькие). 
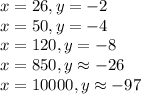
уменьшается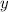 
. Делаем вывод, что функция убывает бесконечно много. То есть 
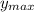— не существует, 
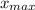— не существует.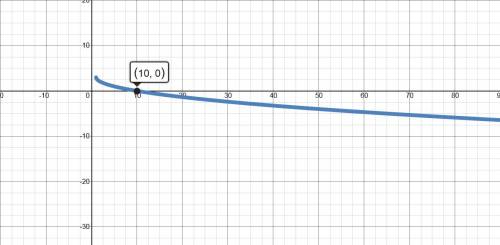 
Пусть один катет х см, тогда другой 17-х см.
Тогда по теореме Пифагора:
х²+(17-х)²=13²
х²+289-34х+х²=169
2х²-34х+120=0
х²-17х+60=0
х=5; х=12.
ответ: 5 см; 12 см.