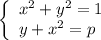
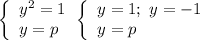
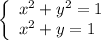
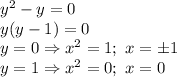
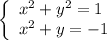
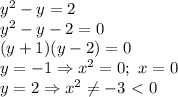
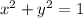Свеча имеет форму правильной четырёхугольной пирамиды с высотой 50 см и стороной основания 7 см. необходимо изготовить коробку той же формы, чтоб её объём был на 2см^3 больше , чем объём свечи. каким при этом будет ребро основания и высота коробки?

👇

Увидеть ответ

Ответ:

grachev791

20.05.2022

Объем пирамиды:

V = SH/3, где S - площадь основания, Н - высота.

Тогда:

V = 7² · 50 : 3 = 816 2/3 (см³)

Объем коробки:

V₁ = V + 2 = 818 2/3 (см³)

Исходя из того, что стенки коробки должны отстоять от стенок свечи на примерно равное расстояние х:

Высота коробки: H₁ = 50 + х см

Площадь основания: S₁ = 49 + x² см²

Тогда: V₁ = (50 + x)(7 + x)² : 3

V₁ = (50 + x)(49 + 14x + x²) : 3

2450 + 700x + 50x² + 49x + 14x² + x³ = 2456

x³ + 64x² + 749x - 6 = 0

Положительный корень уравнения: х ≈ 0,008 (см)

Таким образом, ребро основания коробки х₁ = 7,008 см

высота коробки h = 50,008 см

Таким образом, зазор между стенками коробки и свечой будет сравним с толщиной бытовой алюминиевой фольги и составит 80 микрометров (толщина фольги от 11 до 90 мкм)

4,7(51 оценок)

Открыть все ответы

Ответ:

Grizman7

20.05.2022

$\left\{\begin{array}{l} x^2+y^2=1 \\ y+x^2=p \end{array}$
Заметим, что в системе х встречается только во второй степени. Поэтому, если некоторая пара (х; у) - решение системы, то и пара (-х; у) - решение системы. Так как по заданию система должна иметь только одно решение, то необходимо выполнение условия х=-х. Это достигается только при х=0.
Подставляя значение х=0 в систему, получим:
$\left\{\begin{array}{l} y^2=1 \\ y=p \end{array} \Rightarrw \left\{\begin{array}{l} y=1; \ y=-1 \\ y=p \end{array}$
Проверим, удовлетворяют ли значения р=1 и р=-1 условию.
При р=1:
$\left\{\begin{array}{l} x^2+y^2=1 \\ x^2+y=1 \end{array}$
$y^2-y=0
\\\
y(y-1)=0
\\\
y=0\Rightarrow x^2=1; \ x=\pm1
\\\
y=1\Rightarrow x^2=0; \ x=0$
Данный случай не подходит, так как система имеет три решения.
При р=-1:
$\left\{\begin{array}{l} x^2+y^2=1 \\ x^2+y=-1 \end{array}$
$y^2-y=2 \\\ 
y^2-y-2=0
\\\
(y+1)(y-2)=0
\\\
y=-1\Rightarrow x^2=0; \ x=0
\\\
y=2\Rightarrow x^2 \neq -3\ \textless \ 0$
Данный случай подходит, система действительно имеет одно решение.
Кроме того, можно было построить графики уравнений:
x^2+y^2=1

- окружность с центром в точке (0; 0) и радиусом 1
y=-x^2+p

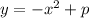- стандартная парабола ветвями вниз с вершиной в точке
(0; р). Двигая эту параболу вдоль оси ординат, можно убедиться, что единственное пересечение с окружностью происходит лишь при р=-1.
ответ: р=-1

4,8(57 оценок)

Ответ:

viktoriafedorip0a2an

20.05.2022

Можно решить графическим

x^2+y^2=R^2 (уравнение

окружности с радиусом R и центром в начале координат)

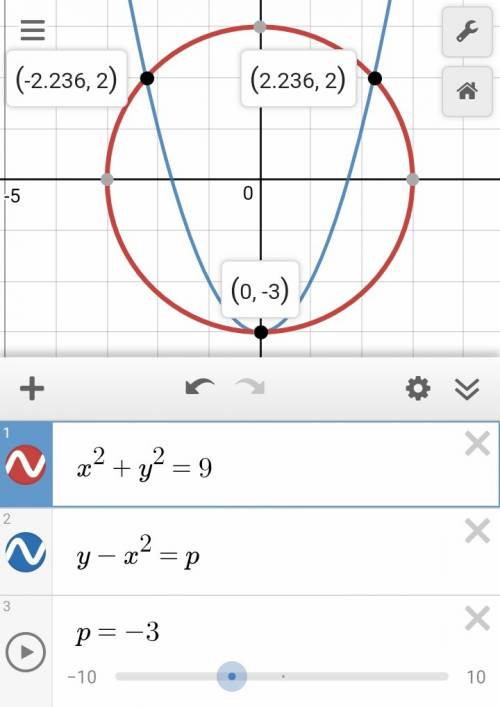
1)Построим грвфик первого уравнения

x^2+y^2=3^2

Координаты центра окружности(0;0);Радиус R=3

2)Построим график второго уравнения

y-x^2=p

y=x^2+p (парабола, ветви вверх, координаты вершины(0;p))

Если p увеличивается, то парабола смещается вверх вдоль оси y и наоборот, если p уменьшается

3) Мы имееем:

- окружность с R=3 с центром в начале координат

- параболу, которая двигается только вдоль оси y, ветви вверх

Мы уже имеем 2 решения благодаря ветвям параболы, которые пересекают окружность в 2-ух точках. Как получить третью точку пересечения(т.е третье решение)? Сместим параболу так, чтобы ее вершина касалась окружности И ветви также продолжали пересекать окружность в 2 точках

Сместим с параболу на -3, т.е вниз на 3 точки(3 потому что радиус окружности также равен 3)

Получим конечный результат(см рис.). 3 решения при p=-3

ответ: p=-3