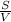, 
= 4 часа — время, потраченное легковой машиной на путь. 
Решим задачу с уравнения. Допустим скорость лодок в стоячей воде равняется х к/час. Тогда, скорость лодки, которая плывет по течению равняется (х + 2) км/час, а скорость лодки, которая плывет против течения составляет (х - 2) км/час. За 2,8 часа лодки встретились и преодолели дистанцию в 212,8 км. Составим уравнение: 2,8 × (х + 2) + 2,8 × (х - 2) = 212,8; 2,8х + 5,6 + 2,8х - 5,6 = 212,8; 5,6х = 212,8; х = 212,8 : 5,6; х = 38. Таким образом, скорость лодок в стоячей воде равняется 38 км/час. Определим скорость лодки, которая плывет по течению: 38 + 2 = 40 км/час; Определим скорость лодки, которая плыла против течения: 38 - 2 = 36 км/час. – материал взят с сайта Студворк https://studwork.org/matematika/158158-rasstoyanie-mejdu-dvumya-pristanyami-ravno-2128-km-iz-nih-odnovremenno-navstrechu-drug-drugu-vyshli-dve-lodki
y`=3x²+10x-4
3x²+10x-4=-7
3x²+10x+3=0
D=100-36=64
x1=(-10-8)/6=-3 y=-27+45+12+132=163
x2=(-10+8)/6=-1/3 y=-1/27+5/9+4/3+132=6 20/27