1.
1) x^2+8x+15=0
Запиши у вигляді суми
x^2+5x+3x+15=0
Розклади вирази на множники
x×(x+5)+3(x+5)=0
Розклади вираз на множники
(x+5)×(x+3)=0
Розклади на можливі випадки
x+5=0
x+3=0
Розв'яжи рівняння
Відповідь: x1 = -5; x2= -3
(Далі робиш по такому же принципу)
2) 2x^2-3x+1=0
2x^2-x-2x+1=0
x×(2x-1)-(2x-1)=0
(2x-1)×(x-1)=0
2x-1=0
x-1=0
Відповідь: x1 = 0,5; x2=1
3) -3x^2+2x+1=0
3x^2-2x-1=0
3x^2+x-3x-1=0
x×(3x+1)-(3x+1)=0
(3x+1)×(x-1)=0
3x+1=0
x-1=0
Відповідь: x1= -1/3; x2= 1
4) x^4+5x^2-36=0
(t=x^2)
t^2+5t-36=0
t= -9
t=4
x^2= -9
x^2= 4
Відповідь: x1= -2; x2= 2
2.
1) x^2-2x-8
x^2+2x-4x-8
x×(x+2)-4(x+2)
(x+2)×(x-4)
2) 2x^2-5x+3
2x^2-2x-3x+3
2x×(x-1)-3(x-1)
(x-1)×(2x-3)
3.
1) x^2+8x-9/2x+18
x^2+9x-x-9/2(x+9)
x×(x+9)-(x+9)/2(x+9)
(x+9)×(x-1)/2(x+9)
x-1/2
2) x^2-2x-8/x^2-16
x^2+2x-4x-8/(x-4)×(x+4)
x×(x+2)-4(x+2)/(x-4)×(x+4)
(x+2)×(x-4)/(x-4)×(x+4)
x+2/x+4
4.
1) m^3+2m^2-8m/m^2+4m
m×(m^2+2m-8)/m×(m+4)
m×(m+4)-2(m+4)/m+4
(m+4)×(m-2)/m+4
m-2
Якщо m = -1, то:
-1-2= -3
Відповідь: -3
Решение 1:
Подставим вместо 'n' в формулу сначала 5, а потом 25:
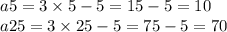
ответ: a5 = 10; a25 = 70
Решение 2:
а3 = 7
а5 = 1
Найдём разность прогрессии по формуле:
d = (a5 - a3)/∆n
в данном случае ∆n = 5-3 = 2
тогда d = (1 - 7)/2 = -3
a(n) находится по формуле:
а(n) = а1 + d(n-1)
в свою очередь а1 = а3 - 2d = 7 + 6 = 13
тогда: а17 = а1 + 16d = 13 - 16*3 = -35
ответ: -35
Решение 3:
По данной в условии формуле находим а1 и а30:
а1 = 3*1+2 = 5
а30 = 3*30+2 = 92
Сумма арифметической прогрессии находится по формуле:
S(n) = (a1+a(n))*n/2
Подставляем вместо 'n' 30:
S30 = (5+92)*30/2 = 97*15 = 1455
ответ: 1455
Решение 4:
а6 = 1
а10 = 13
По формуле d = (a10 - a6)/∆n находим разность прогрессии. В данном случае ∆n = 10 - 6 = 4
тогда: d = (13 - 1)/4 = 3
a1 = a(n) - d(n-1)
a1 = a6 - 5d = 1 - 15 = -14
a20 = a1 + d(n-1)
a20 = -14 + 57 = 43
S(n) = (a1+a(n))*n/2
S20 = (-14 + 43)*20/2 = 29*10 = 290
ответ: 290
Решение 5:
а1 = 20
а2 = 17
а3 = 14
a91 = ?
d = a2 - a1 = 17 - 20 = -3
a(n) = a1 + d*(n-1)
a91 = 20 - 3*90 = -250
ответ: -250
Удачи ^_^