Пусть x - собственная скорость катера, тогда (x-3) - скорость, с которой передвигается катер против течения, а (x+3) - скорость, с которой передвигается катер по течению.
Тогда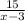 
- время, которое катер плыл против течения, а 
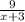- время, которое катер плыл по течению
Полчаса - это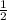 
часа
Из условия задачи следует
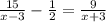
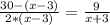
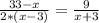
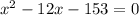
Решаем квадратное уравнение, находим дискриминант:
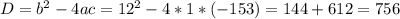
Находим корни:
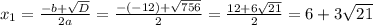
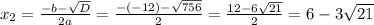
Второй найденный корень - отрицательный, нам не подходит, так как скорость не может быть отрицательной.
Значит, собственная скорость катера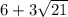 
км/ч
ответ: собственная скорость катера 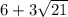км/ч
1) Замена: 2х-7 = m, тогда (2х-7)^2 = m^2
m^2 -11m + 30 = 0
D=121-120=1
x1=(11-1)\2=5
x2=(11+1)\2=6
Подставляем вместо m полученные значения:
2x-7=5 2x-7=6
2x=12 2x=13
x=6 x=6,5
2) Замена: 9-5х = m, тогда (9-5x) = m^2
9m^2 + 17m + 8 = 0
D=289-288=1
x1=(-17+1)\18 = -8\9
x2=(-17-1)\18=-1
Подставляем вместо m полученные значения:
9-5x=-1 9-5x=-8\9
-5x=-10 -5x=-8\9 - 9
x=2 x=89\45
3) Замена: 6x+1=m, тогда (6x+1)^2 = m^2
m^2 +2m -24 = 0
D=4+96=100
x1=(-2-10)\2=-6
x2=(-2+10)\2=4
Подставляем вместо m полученные значения:
6x+1=-6 6x+1=4
6x=-7 6x=3
x=-7\6 x=1\2
4) Замена: 10-3х = m, тогда (10-3x)^2 = m^2
8m^2 -5m -3 = 0
D=25+96=121
x1=(5-11)\16=-3\8
x2=(5+11)\16=1
Подставляем вместо m полученные значения:
10-3x = 1 10-3x = -3\8
-3x=-9 -3x=-3\8 - 10
x=3 x= 83\24
2)y'=(2x-6)'(x²+x+1)+(2x-6)(x²+x+1)'=2(x²+x+1)+(2x-6)(2x+1)=
2x²+2x+2+4x²-10x-6=6x²-8x-4
3)y'=-11/x²