Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a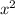
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
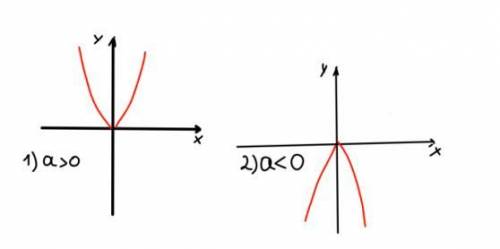
Для этого на примере рассмотрим графики функций у=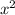 , у=2
, у=2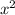 и у=
и у=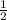
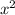
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.
расстояние между двумя городами турист проехал за два дня.В первы день он проехал половину пути и ещё 24км.Во второй день ему осталось проехать расстояние в 3 раза меньшее.чем в 1-ый день. Найдите расстояние между городами.
ответ:96км
Пусть S=x км
первый день -(x/2+24) км
второой день - (x/2+24)/3 км
Получаем уравнение
(x/2+24)+(x/2+24)/3=x
(x+48)/2+(x+48)/6=x-Обе части уравнения умножем на 6
3х+144+х+48=6х
6х-4х=192
2х=192
х=192/2
х=96
ответ :расстояние между городами равно 96 км.