а) sin a * cos a * tg a.
Применим основное тригонометрическое тождество tg a = (sin a)/(cos a), и заменим tg a на (sin a)/(cos a).
sin a * cos a * (sin a)/(cos a).
Сократим cos a и cos a.
sin a * sin a = sin²a.
б) sin a * cos a * ctg a - 1.
По формуле ctg a = (cos a)/(sin a) заменим в данном выражении ctg a.
sin a * cos a * (cos a)/(sin a) - 1.
Сократим sin a и sin a.
cos a * cos a - 1 = cos²a - 1.
Заменим 1 на (sin²a + cos²a), т.к. sin²a + cos²a = 1.
cos²a - (sin²a + cos²a) = cos²a - sin²a - cos²a = -sin²a.
в) sin²a - tg a * ctg a.
Заменим tg a * ctg a на 1, т.к. tg a * ctg a = 1.
sin²a - 1.
Заменим 1 на (sin²a + cos²a).
sin²a - (sin²a + cos²a) = sin²a - sin²a - cos²a = -cos²a.
г) tg a * ctg a + ctg²a.
Заменим (tg a * ctg a) на 1.
1 + ctg²a = 1/sin²a.
Объяснение:
все что я нашел
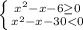
1) x² - x - 6 ≥ 0
(x - 3)(x + 2) ≥ 0
+ - +
______[- 2]______[3]_______
////////////// ////////////////
x ∈ (- ∞ ; - 2] ∪ [3 , + ∞)
2) x² - x - 30 < 0
(x - 6)(x + 5) < 0
+ - +
_______(- 5)______(6)______
///////////////////
x ∈ (- 5 ; 6)
Окончательно :
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ /////////////////////////
______(- 5)_____[- 2]_______[3]_____(6)_____
////////////////////////////////////////////////
ответ : x ∈ (- 5 ; - 2] ∪ [3 ; 6)