Определим общее число расстановок на пяти позициях 5 шариков:
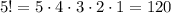
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах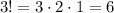 
Таким образом, всего имеется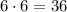 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
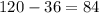
ответ: 84
ответ: 11 2/3 рубля.
Объяснение:
Решение.
Пусть одна тетрадь стоит х рублей.
Тогда Виктор заплатил 17х рублей и у него осталось:
620-17х рублей.
Дарья заплатила 5х рублей и у нее осталось 480-5х рублей.
По условию осталось у них денег поровну.
Составим уравнение:
620-17х = 480-5х;
-17x+5x = 480 - 620;
-12x= - 140;
x= 140/12;
x= 11 2/3 рубля - стоимость одной тетради.
Такое бывает редко, но проверим правильность решения:
620 - 17 * 35/3 = 620 - 595/3 = 421 2/3 рубля.
480 - 5 * 35/3 = 480 - 175/3 = 421 2/3 рубля.
Всё сходится - (странная цена тетради...)
