Ни четная ни нечетная(функция общего вида)
Объяснение:
1) Область определения - вся числовая прямая, это значит, что этот параметр не влияет на четность(функция может быть как четной, так и нечетной, так и общего вида)
2) Функция четна, если f(-x) = f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно f(x), значит функция не может быть четной
3) Функция нечетна, если f(-x) = -f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно -f(x), значит функция не может быть нечетной
4) Таким образом, эта функция ни четная ни нечетная, т.е. эта функция общего вида
1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
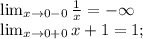
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как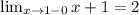 
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: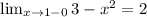 
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
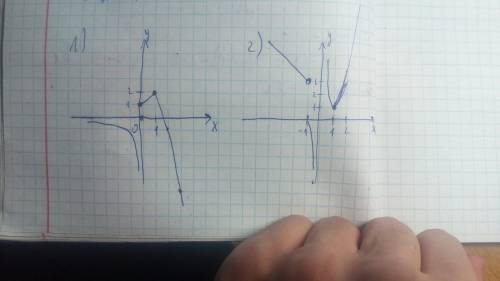
2) Аналогично:
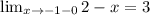
3≠-1, значит -1- это точка разрыва.
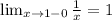
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: 
.
Так как точка х=0 лежит в области определения функции 
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
b1q + b1q^2 = 14 разделим первое уравнение на 2-е
(1 + q^3)/(q +q^2) = -7/2
(1+q)(1 -q +q^2)/q(1 +q) = -7/2
(1 -q +q^2) /q = -7/2
2(1 - q +q^2) = -7q
2 -2q +2q^2 +7q = 0
2q^2 +5q +2 = 0
D = b^2 -4ac = 25 -16 = 9
q1= -1/2, a) b1 + b1q^3 = -49 б) q2 =-2 b1 + b1q^3 = -49
b1 +b1*(-1/8) = -49 b1 + b1*(-8) = -49
7/8 b1 = -49 -7b1 = -49
b1 = -49: 7/8= -49*8/7= =56 b1 = 7