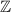разделим на три класса:
, где + обозначает операцию объединения и изначает, что множества 
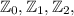дисъюнктны.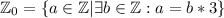
.
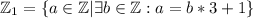
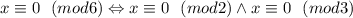
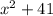делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
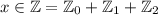, то рассмотрим три случая:
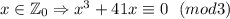так как 
.
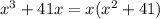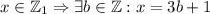
для каких-то 
, то есть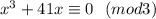 
.
.
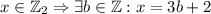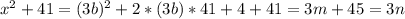для каких-то , то есть .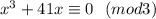
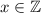выражение 
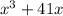делится на 6.
Пусть за х дней может закончить Катя, тогда еѐ производительность равна / х .
А за у дней может закончить Алиса, тогда еѐ производительность равна / у .
Т.к. они могут напечатать курсовую работу за 6 дней,
то /х + /у = 1/
Если сначала % = / части курсовой напечатает Катя,
а затем завершит работу Алиса, то Алисе остается
% = / части курсовой.
Вся курсовая работа будет выполнена за 12 дней т.е.
( /) х + (/ ) у = .
Решим систему:
/х + /у = / ,
(/) х + (/ ) у = .
+ = ,
+ = ;
у = − , ;
+ * ( − , ) = *( − , )
у = − , ;
, ² − + = ;
у = − , ;
² − + = ;
² − + = ;
= , у =
или = , у = . - не подходит, т.к. Катя печатает быстрее, чем Алиса.
Значит, Катя может напечатать курсовую работу за 10 дней.
ответ. за 10 дней
