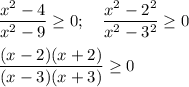
Решим неравенство методом интервалов.
Отмечаем на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. И выкалываем те, что из знаменателя. Мы получили 5 интервала. Перед дробью знак положительный и все множители имею пол. знак при х, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (все множители в нч степени - 1). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая границы.
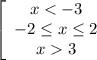
ответ: x ∈ (-∞;-3) ∪ [-2;2] ∪ (3;+∞).
В решении использовалась формула сокращённого умножения: a²-b²=(a-b)(a+b).

Напишем формулу для суммы 9 членов геометрической прогрессии
s9=(b1*(q^9-1))/(q-1)
Напишем формулу для суммы 18 членов геометрической прогрессии
s18=(b1*(q^18-1))/(q-1)
512=2^9
s9/(s18-s9)=2^9
GПеревернем дробь
(s18-s9)/s9=1/2^9
Числитель разделим на знаменатель почленно.
1-s18/s9=1/2^9 Отдельно упростим дробь s18/s9
s18/s9=(b1*(q18-1)/(q-1))/(b1*(q9-1)/(q-1)
Сократятся b1 и (q-1)
s18/s9=(q18-1)/(q9-1) разность квадратов
s18/s9=((q:9-1)*(q^9+1))/(q9-1) Сократим на (q^9-1)
s18/s9=q^9+1
Возвращаемся к уравнению
1-s18/s9=1/2^9
1-q^9+1=1/2^9
-q^9=1/2^9
q=-1/2
4x²-4x+3
4x²-это квадрат числа 2х(это первое число в скобках)
4х - это удвоенное произведение, то есть 2*2х, где 2х- это результат умножения двух чилел
этими числами могут быть 2х и 1; 2 и х; -2х и -1; -2 и -х
так как 2х уже есть, то второе число будет 1.
записываем полученное выражения и ставим знак, который был перед 4х
(2х-1)²=4х²-4х+1
если у нас дано: 4x²-4x+3, то 3 можно расписать как (1+2),получается
4x²-4x+3=4x²-4x+1+2=(4x²-4x+1)+2=(2х-1)²+2
так, например, полный квадрат из выражения х²+6х+8=х²+2*3*х+9-1=
(х²+2*3*х+9)-1=(х+3)²-1