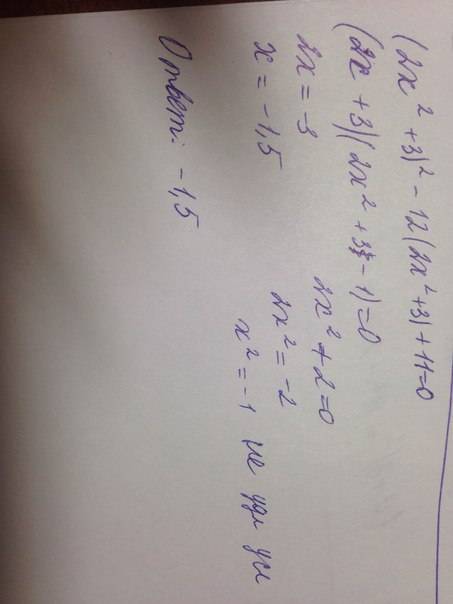
1.2х^2 - 5х+3х^2 + 1-(х – 2).(^это степень)
2х^2 - 5х+3х^2 + 1-х+2=5х^2-6x+3
2.а) -5ху(3х^2 - 0,2у^2 + ху)=-15x^3y+xy^3-5x^2y^2
б)(х – 5)(х + 4)=x^2+4x-5x-20=x^2-x-20
в)(35х^3у - 28х^4) : 7х^3=5y - 4x
3.(р + 3)2 - (3р - 1)(3р + 1=2p+6 -9p^2 - 1=2p-9p^2+5
5.2х^3 – 2(х - 3)(х^2 + 3х + 9)=x^3-(x-3)*(x^2+3x+9)=x^3-x^3-3x^2-9x+3x^2+9x+27=27
Этим мы доказали ,что результат не зависит от переменной
4.Первое число - х
Второе число - х+1
Третье число - х+2
Составляем уравнение:
(x+1)(x+2)-x^2=47
x^2+2x+x+2-x^2=47
3x=45
x=15 - первое число
15+1=16 - второе число
15+2=17 - третье число
Проверка:16*17-15^2=272-225=47
ответ: 7,5 км.
Объяснение:
Дано. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия.
На какое расстояние от лагеря они отплыли
если скорость течения реки равна 2 км/ч,
а собственная скорость лодки 8км час.
Решение.
Пусть расстояние до причаливания равна х км.
Скорость лодки против течения равна 8-2=6 км/час.
Скорость лодки по течению равна 8+2=10 км/час
Время на прохождение пути по течению равно t1=S/v= x/6 часов
Время на преодоления по течению равно t2=x/10 часов .
На весь путь они потратили 5 - 3=2 часа.
Составим уравнение:
х/6 + х/10 = 2;
5х + 3х =60;
8х=60;
х= 7,5 км от начала путешествия до причаливания.
Проверим:
7,5/6 + 7,5/10 = 2;
1,25 + 0,75 = 2 часа - всё верно!