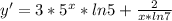
2sin2x + 3sinxcosx - 3cos2x = 1;
Представим 1 в виде суммы по основному тригонометрическому тождеству:
sin2x + 3cosxsinx - 3cos2x = sin2x + cos2x;
Приведем подобные:
sin2x + 3cosxsinx - 4cos2x = 0;
Разделим каждый член уравнения на cos2x:
tg2x + 3tgx - 4 = 0;
Произведем замену и решим квадратное уравнение:
t2 + 3t - 4 = 0;
D = 9 + 16 = 25;
t = (-3 +- 5)/2;
t1 = -4, t2 = 1;
Сделаем обратную замену:
tgx = 1; x = pi/4 + pin, n из Z;
tgx = -4; x = arctg(-4) pin, n из Z.
ответ: pi/4 + pin, n из Z; arctg(-4) pin, n из Z.
Объяснение:
Оцени!
формула из комбинаторики,
мы рассматриваем любое из 10 цифр, а формула для конкретной определенной цифры, поэтому
10*C₆⁴=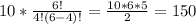
Кроме того остались другие два числа, принимающие любые значения, кроме той определенной цифры(9 из 10, в двух разных независимых местах) это 9²=81.
81*150=12150 вариаций
2) модератор подсказал, что число 011119 - не шестизначное, т.к. начинается с нуля, поэтому пусть будет две задачки. Кто знает, что имел в виду задававший вопрос, учитывал или нет этот факт про нули впереди? В одном мы не обращаем на это внимание, и это решение выше. Ниже обратим внимание и решим чуть иначе.
Сначала мы рассматривали числа от 0 до 999999, теперь рассмотрим числа от 100000 до 999999, так всё что ниже не шестизначные цифры. Мы отбросили числа ниже 100000, тоесть осталось ровно 90% от первоначальных чисел, т.к. это перебор всех возможных цифр, то распределение цифр и в самой последовательности от 0 до 999999 и в 100000 до 999999 равновероятны. Так и случайно взятые на угад 4 одинаковые цифры из 6, также равнораспределены на обоих этих отрезках непрерывной последовательности натуральных чисел. Отсюда можно сделать вывод, что нами полученный ответ в первой задаче умноженный на 90% и есть ответ на вторую задачу 12150*0.9=10935