1/x(x+4)+1/(x+4)(x+8)+1/(x+8)(x+12)+1/(x+12)(x+16)
ну можно все привести к общему знаменателю, и потом возиться с шестой степенью в числителе
а можно обратить внимание,что
1/n(n+4) = 1/4 * 4/n(n+4) = 1/4(n+4-n)/n(n+4) = 1/4*(1/n - 1/(n+4))
это выполняется для всех х, для которых разница в знаменателе = 4
1/(n+1)(n+5), 1/(n+8)(n+12), 1/(n+100)(n+104) итд
1/4* ( 1/x - 1/(x+4) + 1/(x+4) - 1/(x+8) + 1/(x+8) - 1/(x+12) + 1/(x+12) - 1/(x+16)) = 1/4*(1/x - 1/(x+16)) = 1/4*(x+16 - x)/x(x+16) = 1/4* 16/x(x+16) = 4/x(x+16)
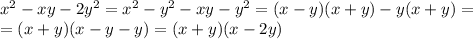
Мы разложили левую часть на два множителя. Число 7 — простое, поэтому оно может раскладываться ровно на две пары целых множителей: (1; 7) и (–1, –7). Тогда получим четыре системы:
Первая система:
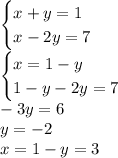
Вторая система:
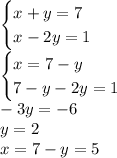
Третья система:
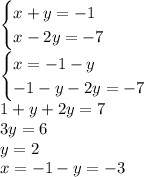
Четвёртая система:
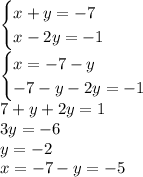
ответ: (3; –2), (–3; 2), (5; 2), (–5; –2).
P. S. Третью и четвёртую систему можно было бы не расписывать, если заметить, что при одновременной замене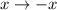 
и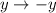 
значение выражения 
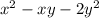не изменится. Это означает, что если (x; y) является решением, то (–x; –y) тоже является решением.
4x²-4x-8=2x-1+4x²-2x-6x
-4x-2x+6x+2x=-1+8
2x=7
x=3.5
-5y+(3y+4)(3y-4)=(4y-3)(3+4y)-7y^2
-5y+9y²-16=16y²-9-7y²
9y²-16y²+7y²-5y=-9+16
-5y=7
y=-5/7
вроде так