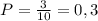
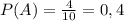
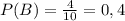
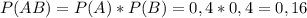
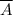 и найдём его вероятность.
и найдём его вероятность.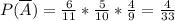
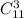 ). И вычислить число вариантов выбора 3 нарциссов из 6 (
). И вычислить число вариантов выбора 3 нарциссов из 6 ( ). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.
). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.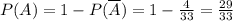
 х - 2.
х - 2.
-1=9+3b+c
решаем системой
8=с
-1=9+3b+8
ниже системы находим b
-1=9+3b+8
-1-9-8=3b
-18=3b
-6=b
ответ: b=-6, c=8