Представить вырожение в виде многочлена стандартного вида (а-7)^2+(а-3)(а+3)-18а

👇

Увидеть ответ

Ответ:

Neznaikakrasno

13.04.2023

=a^2+49-14a+a^2-9-18a=2a^2+40-32a

4,7(45 оценок)

Ответ:

макс240723212321

13.04.2023

А^2-14а+49+а^2-9-18а=2а^2-32а+40

4,6(71 оценок)

Открыть все ответы

Ответ:

лёха562

13.04.2023

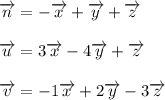
$\overrightarrow{n}=-\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}\\ \\ \overrightarrow{u}=3\overrightarrow{x}-4\overrightarrow{y}+\overrightarrow{z}\\\\\overrightarrow{v}=-1\overrightarrow{x}+2\overrightarrow{y}-3\overrightarrow{z}$

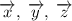В базисе $\overrightarrow{x},\;\overrightarrow{y},\;\overrightarrow{z}$ векторы имеют следующие координаты:

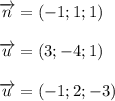
$\overrightarrow{n}=(-1; 1;1)\\ \\ \overrightarrow{u}=(3; -4;1)\\ \\ \overrightarrow{u}=(-1; 2;-3)\\ \\$

Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.

Докажем компланарность векторов двумя

школьный (≈10 класс)

Признак компланарности трёх векторов:

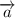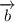Пусть векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ не коллинеарны. Если для вектора 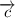$\overrightarrow{c}$ существует единственная пара реальных чисел A и B, такая, что 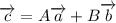$\overrightarrow{c}=A\overrightarrow{a}+B\overrightarrow{b}$ , то векторы 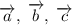$\overrightarrow{a},\;\overrightarrow{b},\;\overrightarrow{c}$ компланарны.

Покажем, что

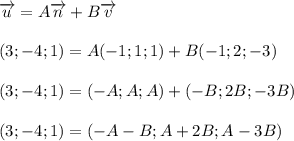
$\overrightarrow{u}=A\overrightarrow{n}+B\overrightarrow{v}\\ \\ (3;-4;1)=A(-1;1;1)+B(-1;2;-3)\\ \\ (3;-4;1)=(-A;A;A)+(-B;2B;-3B)\\ \\ (3;-4;1)=(-A-B;A+2B;A-3B)$

Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:

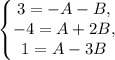
$\left\{\begin{matrix}3=-A-B,\\ -4=A+2B,\\ 1=A-3B\end{matrix}\right.$

Сложим первое и второе уравнение, получим:

-1 = B

Подставим значение B в первое уравнение, найдём A:

3 = -A - (-1)

A = -2

Проверим найденные значения для остальных уравнений системы.

Итого получаем:

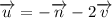
$\overrightarrow{u}=-\overrightarrow{n}-2\overrightarrow{v}$

То есть признак выполнен. Значит векторы компланарны.

обычно проходится в вузах):

Векторы 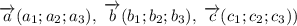$\overrightarrow{a}(a_1;a_2;a_3),\;\overrightarrow{b}(b_1;b_2;b_3),\;\overrightarrow{c}(c_1;c_2;c_3))$ компланарны, если

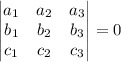
$\begin{vmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1& c_2 & c_3\end{vmatrix}=0$

Проверим это условие для данных векторов:

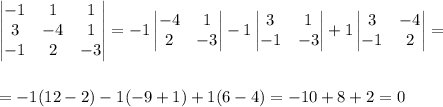
$\begin{vmatrix} -1& 1 & 1\\ 3 & -4 & 1\\ -1 & 2 & -3\end{vmatrix}=-1\begin{vmatrix} -4 & 1\\ 2 & -3\end{vmatrix}-1\begin{vmatrix}3 & 1\\ -1 & -3\end{vmatrix}+1\begin{vmatrix}3 & -4 \\ -1 & 2 \end{vmatrix}=\\ \\\\ =-1(12-2)-1(-9+1)+1(6-4)=-10+8+2=0$